Intégrale difficile
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
TonyPi
- Messages: 3
- Enregistré le: 28 Oct 2008, 11:23
-
 par TonyPi » 28 Oct 2008, 11:36
par TonyPi » 28 Oct 2008, 11:36
Bonjour à tous,
J'ai une intégrale à résoudre mais je ne vois pas comment m'y prendre
La voici :
Soit f(x)=[intégrale entre 0 et pi/2 de..](dt/(1+xsint))
Montrer que f(x)=2*[intégrale de 0 à 1 de..](du/(u²+2ux+1))
Puis montrer que f(x)=[intégrale de 0 à +infini de..](dv/(v²+2vx+1))
Désolé pour le format, je ne sais pas comment écrire les intégrales avec un clavier.
Merci de votre aide.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 28 Oct 2008, 13:29
par Joker62 » 28 Oct 2008, 13:29
Bonjour ;)
Pour le passage de la 1ère à la 2ème il faut se rappeler d'une technique qui marche quasiment toujours quand il se trouve des fonctions trigo : Les règles de Bioche
Ici le changement t = tan(u/2) donne le résultat.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 28 Oct 2008, 13:55
par Pythales » 28 Oct 2008, 13:55
Poser

pour la 1ère, puis
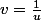
pour la 2ème
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 28 Oct 2008, 14:06
par Joker62 » 28 Oct 2008, 14:06
Par contre j'ai un gros doute sur le pi/2 dans la borne de la première intégrale :) J'aurais vu pi/4 moi
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 28 Oct 2008, 14:29
par Pythales » 28 Oct 2008, 14:29
Si

, pour
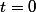
on a
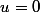
et pour

on a
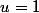
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 28 Oct 2008, 14:55
par Joker62 » 28 Oct 2008, 14:55
J'ai mélangé t et u dans ma formule :D
désolé :)
-
TonyPi
- Messages: 3
- Enregistré le: 28 Oct 2008, 11:23
-
 par TonyPi » 29 Oct 2008, 11:34
par TonyPi » 29 Oct 2008, 11:34
merci a vous ! :we:
encore une question : :zen:
comment on montre que f est décroissante ?
merci de votre réponse
 par busard_des_roseaux » 29 Oct 2008, 15:29
par busard_des_roseaux » 29 Oct 2008, 15:29
TonyPi a écrit:merci a vous ! :we:
encore une question : :zen:
comment on montre que f est décroissante ?
merci de votre réponse
ces intégrales ont été calculées sur l'autre fil. Pourquoi du multipostage ?
ceçi écrit, f est décroissante car sin est une fonction positive
sur l'intervalle d'intégration. Les inégalités sont conservées,sauf lors du passage à l'inverse.
-
Tyty
- Messages: 1
- Enregistré le: 30 Oct 2008, 12:01
-
 par Tyty » 30 Oct 2008, 12:05
par Tyty » 30 Oct 2008, 12:05
Pythales a écrit:Poser

pour la 1ère, puis
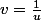
pour la 2ème
Bonjour.
en posant
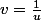
, je ne vois pas comment on arrive aux bornes 0 et +l'infini.
Pourriez vous m'expliquer plus précisément la méthode ? merci
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 30 Oct 2008, 13:44
par Joker62 » 30 Oct 2008, 13:44
Part de la dernière tu la découpe en deux intégrales une de 0 à 1 et l'autre de 1 à l'infini
Dans la deuxième fait le changement de variable et retrouve la première
Edit : Pourquoi autant de pseudo ? :^)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 159 invités
