Intégrale à deux paramètres
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
par Aspx » 08 Nov 2007, 16:14
Bonsoir,
On se donne une fonction continue sur R+ et f(t)/t est supposée pseudo-intégrable en l'infini. Pour tous a,b>0 montrer que la pseudo intégrale
-f(a t) \frac {dt}{t})
existe et la calculer.
Ok pour l'existence, pour le calcul j'ai calculé les paquets de Cauchy (considérant a<b) :
-f(a t) \frac {dt}{t} = \int_{bx}^{by}\frac{f(t)}{t}dt - \int_{ax}^{ay}\frac{f(t)}{t}dt<br />\\ = \int_{ax}^{bx}\frac{f(t)}{t}dt + \int_{ay}^{by}\frac{f(t)}{t}dt = \int_{a}^{b}\frac{f(t x)}{t}dt + \int_{a}^{b}\frac{f(t y)}{t}dt)
Donc voilà j'ai cherché mais bon ça mène un peu à rien... Une idée ?
Merci d'avance!
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
par Pythales » 08 Nov 2007, 17:52
\frac{dt}{t}=\int_0^{\infty}f(u)\frac{du}{u})
en posant
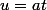
La réponse est zéro
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
par Aspx » 08 Nov 2007, 17:56
C'est ce que je me suis dit mais je trouvais ça trop gros pour être vrai :we:
Merci !
-
totom
- Membre Naturel
- Messages: 33
- Enregistré le: 24 Oct 2007, 11:50
-
par totom » 08 Nov 2007, 20:40
Je disais donc f(0) ln(a/b).
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
par Aspx » 08 Nov 2007, 20:50
Cela tend vers 0 ou pas ? Le premier morceau (de la fin de mon calcul) semble tendre vers ce que tu annonce totom, mais le second morceau ? :hein:
-
totom
- Membre Naturel
- Messages: 33
- Enregistré le: 24 Oct 2007, 11:50
-
par totom » 08 Nov 2007, 21:00
désolé pour mes messages intempestifs...
En fait tu peut faire tendre y vers l'infini dans le second morceau et ça fait 0, et pour le premier(ou tu as inversé les bornes je crois), une petite formule de la moyenne te donne f(c)ln(b/a) ou c strictement compris entre bx et ax , et par continuité de f quand x tend vers 0, voili voilou!
De plus à moins que a=b, ça n'a pas de raison de faire 0 géometriquement.
En esperant avoir été utile.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
