Intégrale à deux paramètres le retour

[Aspx]

Bonsoir,
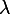
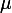
et sont deux réels strictement positifs. Calculer (existence ok) :


On ne peut séparer en deux et faire un changement de variable car l'intégrale cesse d'exister (car non intégrable en 0).
Alors comment procéder ?

Merci d'avance.

[ThSQ]

Et si on procédait comme ça :

..... on coupe en deux + changement de variables = quand

[Aspx]

Niquel ! L'astuce du x rah :we:
Je retiendrai ! Merci beaucoup ThSQ !

[totom]

Salut,
je suis tout a fait d'accord avec ce résultat, ce qui te démontre qu' en général ça fait pas zéro comme cela a pu etre dit.
Pour le cas général avec f, je trouve f(0) ln(mu/lambda)...sauf erreur.
A plus :we:

[Aspx]

totom dans l'autre post on peut séparer car ça continue d'exister j'ai l'impréssion... Enfin bref :we:

[Pythales]

Soit
En intégrant d'abord par rapport à :
En intégrant d'abord par rapport à :
NB. Ici, en séparant en 2, on a la forme alors que dans l'autre post, on avait la forme