Bonjour,est ce que vous pouvez m'expliquez comment calculer une integrale curviligne de facon generale(je n'ai pas de cours dessus) puis me dire comment je dois le faire sur mon probleme
calcul de l'integrale curviligne du champ V=(2xy+y²-1,2xy+x²)sur le segment A(1,0) vers B(0,1).
Merci
Integrale curviligne
6 messages
- Page 1 sur 1
praud a écrit:Bonjour,est ce que vous pouvez m'expliquez comment calculer une integrale curviligne de facon generale(je n'ai pas de cours dessus) puis me dire comment je dois le faire sur mon probleme
calcul de l'integrale curviligne du champ V=(2xy+y²-1,2xy+x²)sur le segment A(1,0) vers B(0,1).
Merci
Salut,
Sans grande convicton:
r:R -> RxR
r(t) = (1-t,t)
Puis:
praud a écrit:Je n'ai pas compris ce que tu fais?
La fonction r(t) paramètre le segment AB pour t dans [0,1].
Ensuite j'applique la formule donnée ici pour un champ vectoriel.
bjr,
je crois, :hum: , qu'il suffit d'intégrer:
dx + V_{2}(x,y) dy)
et on paramètre le chemin par
par
,y(t)))
c ok, "ma" définition coïcide avec celle de Jean-luc, car le . est le produit scalaire de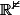
La différentielle V(r).r' que tu intégre est fermée (elle vérifie
la condition de Schwarz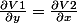
et ce que l'on intégre est donc une différentielle d'une application de [0;1] dans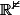
je crois, :hum: , qu'il suffit d'intégrer:
et on paramètre le chemin
c ok, "ma" définition coïcide avec celle de Jean-luc, car le . est le produit scalaire de
La différentielle V(r).r' que tu intégre est fermée (elle vérifie
la condition de Schwarz
et ce que l'on intégre est donc une différentielle d'une application de [0;1] dans
mathelot a écrit:La différentielle V(r).r' que tu intégre est fermée (elle vérifie
la condition de Schwarz
as tu remarqué que ton champs de vecteur V sont les coordonnées
de la différentielle de l'application
et donc que , quand on paramètre par t, puis le produit scalaire avec r'(t), on trouve tout simplement
la dérivée d'une fonction de
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
