Bonsoir,
Est ce que l'intervalle curviligne le long d'une courbe C est égale à la circulation le long de C ?
Je sais qu'il y en a un qu'on utilise pour le champ sclaire et l'autre pour le champ vectoriel . Mais est ce que ces intégrales valent la même valeurs ?
Intégrale curviligne et Circulation
8 messages
- Page 1 sur 1
Salut, la question n'est pas très claire... Comme tu l'as dit, on ne fait circuler que des champs vectoriels, alors qu'on peut intégrer des champs aussi bien vectoriels que scalaires le long d'un chemin. Si je me donne un champ vectoriel X sur un chemin gamma, tu veux comparer la circulation de X à l'intégrale de quel champ scalaire ?
Dans ce cas c'est non. Par exemple tu prends f(x,y) = 1 un potentiel scalaire constant : le champ vectoriel dérivé est identiquement nul mais l'intégrale de f sur une courbe n'a aucune raison de l'être. De plus, il existe des champs vectoriels qui ne dérivent pas d'un potentiel scalaire (exemple typique en physique : le champ magnétique).
En revanche, si f est un champ scalaire, on a - f(a)) où a et b sont les extrémités du chemin
où a et b sont les extrémités du chemin  : la circulation du champ dérivé s'exprime facilement, sans intégrale, à l'aide de f, ce qui n'est pas très surprenant puisque f est un genre de primitive.
: la circulation du champ dérivé s'exprime facilement, sans intégrale, à l'aide de f, ce qui n'est pas très surprenant puisque f est un genre de primitive.
En revanche, si f est un champ scalaire, on a
En faisant l'analogie en physique, f ça peut être la fonction potentiel que je préfère appelé V.
Et E = - grav V c'est le champ éléctrique c'est un champ de vecteur qui dérive d'un potentiel.
Quand je fais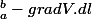 qui est un porduit sclaire , j'obtiens bien V(a)-V(b). Or V(a)-V(b) je croyais que c'était aussi égale à l'intégrale curviligne de la forme différentielle dV de a à b.
qui est un porduit sclaire , j'obtiens bien V(a)-V(b). Or V(a)-V(b) je croyais que c'était aussi égale à l'intégrale curviligne de la forme différentielle dV de a à b.
-grad V (x,y) est un vecteur et dl=(dx,dy) un autre vecteur donc en faisant le produit de ces deux vecteurs on obtient un produit scalaire (travail pour une charge unité en physique)
Si je comprend bien, l'intégrale curviligne dont tu croyais que je parlais était celle qui revient à intégrer la fonction potentiel V ? c'est a dire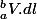 avec V et dl des scalaires
avec V et dl des scalaires
Et E = - grav V c'est le champ éléctrique c'est un champ de vecteur qui dérive d'un potentiel.
Quand je fais
-grad V (x,y) est un vecteur et dl=(dx,dy) un autre vecteur donc en faisant le produit de ces deux vecteurs on obtient un produit scalaire (travail pour une charge unité en physique)
mais l'intégrale de f sur une courbe n'a aucune raison de l'être
Si je comprend bien, l'intégrale curviligne dont tu croyais que je parlais était celle qui revient à intégrer la fonction potentiel V ? c'est a dire
Quand on parle de l'intégrale d'une fonction suivant une courbe, c'est de l'intégrale de cette fonction qu'on parle, pas de l'intégrale de sa dérivée ou de sa différentielle. Aussi, faut faire gaffe si tu veux utiliser des notations de physique dans un cadre purement mathématique, surtout au niveau des dépendances par rapport aux variables.
En prenant les notations habituelles en physique, oui, on a bien - V(b)) , ça découle directement de la définition du gradient qui dit (avec des notations physiques, encore une fois) que
, ça découle directement de la définition du gradient qui dit (avec des notations physiques, encore une fois) que  , mais ça n'a rien à voir avec l'intégrale curviligne de V.
, mais ça n'a rien à voir avec l'intégrale curviligne de V.
En prenant les notations habituelles en physique, oui, on a bien
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
