Salut,
Yezu a écrit:Je me demandais ainsi, si passer par la valeur principale de Cauchy était le meilleur moyen de contourner cette difficulté.
Perso, cette histoire de "valeur principale", c'est un truc que j'ai jamais bien compris (pas les résultats qui en découle, mais l'intérêt d'une telle notion).
Tout ce que je peut te dire, c'est que la question n'est absolument pas de savoir si "
de passer par la valeur principale est malin ou pas" : si tu prend cette intégrale au sens usuel des intégrales, alors il n'y a pas photo, elle est divergente et puis c'est tout. Par contre, si on considère cette intégrale
au sens de la valeur principale, alors oui, tu peut lui attribuer une valeur (*)
(*) Mais quand à savoir si c'est futé ou pas d'écrire que "intégrale=la_valeur_en_question", c'est là que je suis pas sûr que ce soit futé vu que cette nouvelle définition ne possède pas certaines propriétés "usuelles" des intégrales. Par exemple ça ne vérifie évidement plus la relation de Chasles si on "coupe" l'intégrale à l'endroit où ce n'est pas intégrable.
Sur
Wiki, ils disent bien que dans ce cas, ce n'est pas
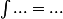
qu'on doit écrire, mais
=...)
histoire d'éviter d'écrire des conneries...
P.S. Sur Wiki, on peut aussi lire concernant la valeur principale de l'intégrale de 1/x^3 entre -1 et 1 que :
Ce qui correspond à l'intuition puisque la fonction est impaire et que l'on intègre sur un intervalle symétrique. Et je me demande un peu ce qu'il a comme "intuition" le type qui a écrit ça vu que la mienne, ce qu'elle me dicte surtout, c'est que c'est prendre un très très gros risque que de vouloir mordicus attribuer une valeur finie à cette intégrale là...
