Intégrale et aire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Mar 2015, 16:25
par mehdi-128 » 13 Mar 2015, 16:25
Bonjour,
Je comprends pas pourquoi
 dB$$)
correspond à la surface intérieure du cyle hystérésis ci-dessous :

Cordialement.
Merci.
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 13 Mar 2015, 17:22
par Manny06 » 13 Mar 2015, 17:22
mehdi-128 a écrit:Bonjour,
Je comprends pas pourquoi
 dB$$)
correspond à la surface intérieure du cyle hystérésis ci-dessous :

Cordialement.
Merci.
Il s'agit plutôt de Physique
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 13 Mar 2015, 17:33
par mehdi-128 » 13 Mar 2015, 17:33
Manny06 a écrit:Il s'agit plutôt de Physique
Non ma question est sur l'intégrale.
J'essaie de comprendre pourquoi elle correspond à l'aire intérieure et ça c'est des maths.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 13 Mar 2015, 21:58
par Pisigma » 13 Mar 2015, 21:58
mehdi-128 a écrit:Non ma question est sur l'intégrale.
J'essaie de comprendre pourquoi elle correspond à l'aire intérieure et ça c'est des maths.
Voici un fichier attaché
http://www.cjoint.com/data/0Cnv3lwxc14_cycle_hysteresis.pngEt quelques explications:

S1 correspond au déplacement entre le point 1 et 2 H>0, dB >0 Hdb>0 et S1>0
S2 correspond au déplacement entre le point 2 et 3 H>0, dB 0 et S3>0
S4 correspond au déplacement entre le point 4 et 1 H0 Hdb<0 et S4<0
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 14 Mar 2015, 04:38
par mehdi-128 » 14 Mar 2015, 04:38
[quote="Pisigma"]Voici un fichier attaché
http://www.cjoint.com/data/0Cnv3lwxc14_cycle_hysteresis.pngEt quelques explications:

S1 correspond au déplacement entre le point 1 et 2 H>0, dB >0 Hdb>0 et S1>0
S2 correspond au déplacement entre le point 2 et 3 H>0, dB 0 et S3>0
S4 correspond au déplacement entre le point 4 et 1 H0 Hdb0 ou dB < 0 ?
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 14 Mar 2015, 07:45
par Pisigma » 14 Mar 2015, 07:45
[quote="mehdi-128"]Merci beaucoup, je pense comprendre l'idée, ça veut dire quoi le dB 0 ou dB 0 si on se déplace dans le sens des flèches = dans le sens positif de l'axe 0B.
dB <0 si on se déplace dans le sens contraire des flèches = dans le sens négatif de l'axe 0B.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 14 Mar 2015, 08:43
par Pisigma » 14 Mar 2015, 08:43
Pisigma a écrit:Bonjour,
dB >0 si on se déplace dans le sens des flèches = dans le sens positif de l'axe 0B.
dB <0 si on se déplace dans le sens contraire des flèches = dans le sens négatif de l'axe 0B.
Si tu le souhaites, je peux redessiner les courbes autrement de façon à faire apparaître les différences par intégration entre les 2 courbes. Mais pas avant ce soir, car maintenant c'est impossible pour moi.
-
Fazyl
- Messages: 1
- Enregistré le: 14 Mar 2015, 08:45
-
 par Fazyl » 14 Mar 2015, 08:52
par Fazyl » 14 Mar 2015, 08:52
Bonjours a Tous
j'ai un petit problemme avec c'est 3 intégrales si vous pouvais m'aider sa serai tré simpa :we:
1) :Int: cos(x)/(2-cos²(x))
2) :int: (exp(2x)-1)/(exp(2x)+1)
3):int: (arctang(x))/(1-x²)^1/2)
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 14 Mar 2015, 09:41
par Pisigma » 14 Mar 2015, 09:41
Fazyl a écrit:Bonjours a Tous
j'ai un petit problemme avec c'est 3 intégrales si vous pouvais m'aider sa serai tré simpa :we:
1) :Int: cos(x)/(2-cos²(x))
2) :int: (exp(2x)-1)/(exp(2x)+1)
3):int: (arctang(x))/(1-x²)^1/2)
Tu dois poster et pas t' insérer dans le post d'un autre :mur:
-
mathelot
 par mathelot » 14 Mar 2015, 11:47
par mathelot » 14 Mar 2015, 11:47
Fazyl a écrit:Bonjours a Tous
j'ai un petit problemme avec c'est 3 intégrales si vous pouvais m'aider sa serai tré simpa :we:
1) :Int: cos(x)/(2-cos²(x))
2) :int: (exp(2x)-1)/(exp(2x)+1)
3):int: (arctang(x))/(1-x²)^1/2)
cette conversation se poursuit
ici
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 14 Mar 2015, 17:51
par mehdi-128 » 14 Mar 2015, 17:51
Pisigma a écrit:Bonjour,
dB >0 si on se déplace dans le sens des flèches = dans le sens positif de l'axe 0B.
dB <0 si on se déplace dans le sens contraire des flèches = dans le sens négatif de l'axe 0B.
Je pensais que le dB était toujours positif comme le dx quand on prend une variation infiniment petite de x.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 14 Mar 2015, 17:56
par mehdi-128 » 14 Mar 2015, 17:56
Pisigma a écrit:Si tu le souhaites, je peux redessiner les courbes autrement de façon à faire apparaître les différences par intégration entre les 2 courbes. Mais pas avant ce soir, car maintenant c'est impossible pour moi.
Merci beaucoup ! Oui je veux bien

Le premier schéma qui m'aide déjà beaucoup visuellement on voit que l'aire vaut : (S1 - S2) + (S3 - S4)
C'est plus intuitif pour moi que les aires négatives.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 14 Mar 2015, 21:00
par Pisigma » 14 Mar 2015, 21:00
mehdi-128 a écrit:Merci beaucoup ! Oui je veux bien

Le premier schéma qui m'aide déjà beaucoup visuellement on voit que l'aire vaut : (S1 - S2) + (S3 - S4)
C'est plus intuitif pour moi que les aires négatives.
Comme convenu, voilà en attaché, un fichier avec des courbes dessinées "de manière habituelle"
http://www.cjoint.com/data/0CovftUIKy6.htm 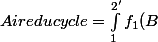dB-\int_3^{2'}f_2(B)dB-\int_{4'}^3f_2(B)dB+\int_{4'}^1 f_1(B)dB)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 15 Mar 2015, 00:57
par mehdi-128 » 15 Mar 2015, 00:57
Merci c'est super clair j'ai tout compris mais vous avez représenté H = f(B) au lieu de B = f(H) sur ma figure initiale mais ça change rien je suppose ?
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 15 Mar 2015, 03:36
par mehdi-128 » 15 Mar 2015, 03:36
Sinon elle vient d'où cette formule ?
C'est une formule générale ?

S1 correspond au déplacement entre le point 1 et 2 H>0, dB >0 Hdb>0 et S1>0
S2 correspond au déplacement entre le point 2 et 3 H>0, dB 0 et S3>0
S4 correspond au déplacement entre le point 4 et 1 H0 Hdb<0 et S4<0
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 15 Mar 2015, 08:46
par Pisigma » 15 Mar 2015, 08:46
mehdi-128 a écrit:Merci c'est super clair j'ai tout compris mais vous avez représenté H = f(B) au lieu de B = f(H) sur ma figure initiale mais ça change rien je suppose ?
C'est parce que l'aire du cycle représente l'énergie dégagée (par unité de volume) quand on décrit le cycle.

, formule analogue à

-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 15 Mar 2015, 08:48
par Pisigma » 15 Mar 2015, 08:48
mehdi-128 a écrit:Sinon elle vient d'où cette formule ?
C'est une formule générale ?

S1 correspond au déplacement entre le point 1 et 2 H>0, dB >0 Hdb>0 et S1>0
S2 correspond au déplacement entre le point 2 et 3 H>0, dB 0 et S3>0
S4 correspond au déplacement entre le point 4 et 1 H0 Hdb<0 et S4<0
Ce n'est pas une formule générale, mais elle est donnée dans tous les cours élémentaire de magnétisme.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 16 Mar 2015, 16:11
par mehdi-128 » 16 Mar 2015, 16:11
Pisigma a écrit:Ce n'est pas une formule générale, mais elle est donnée dans tous les cours élémentaire de magnétisme.
C'est parce que généralement les intégrales normales y a des bornes et là c'est une intégrale fermée sur un contour...
Sinon j'avais un autre truc que j'arrive pas à comprendre le changement de borne de l'intégrale alors qu'on a juste remplacé v(t) par sa valeur et simplifié :
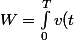i(t) dt)
Avec
= \frac{Nd\Phi(t)}{dt})
D'où :
}{dt}i(t) dt=\int_{cycle} Ni(t) d\Phi)
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 16 Mar 2015, 22:03
par Pisigma » 16 Mar 2015, 22:03
mehdi-128 a écrit:C'est parce que généralement les intégrales normales y a des bornes et là c'est une intégrale fermée sur un contour...
Sinon j'avais un autre truc que j'arrive pas à comprendre le changement de borne de l'intégrale alors qu'on a juste remplacé v(t) par sa valeur et simplifié :
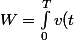i(t) dt)
Avec
= \frac{Nd\Phi(t)}{dt})
D'où :
}{dt}i(t) dt=\int_{cycle} Ni(t) d\Phi)
Difficile de répondre à ta question avec précision car je ne connais pas tout le développement mais
dt se simplifie donc tu ne peux plus intégrer sur une période T. La variation de flux a lieu sur un cycle.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 18 Mar 2015, 14:55
par mehdi-128 » 18 Mar 2015, 14:55
Pisigma a écrit:Difficile de répondre à ta question avec précision car je ne connais pas tout le développement mais
dt se simplifie donc tu ne peux plus intégrer sur une période T. La variation de flux a lieu sur un cycle.
Le cycle c'est la courbe B = f(H) ...
Or :

donc

Le flux est proportionnel à B donc intégrer par rapport à Phi revient au même qu'intégrer par rapport à B dans les bornes de l'intégrale ?
Le problème c'est qu'en physique les changement de variable sont faits un peu à l'arrache.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités