Intégrale de sin(x) via calcul d'aire

[Studenthec]

Je cale un peu sur ce procédé en ce qui concerne les trigonométriques, j'ai réussi à faire toutes les autres fonctions mais les trigonométriques, ça coince.

Ce n'est évident pas le calcul des intégrales via les primitives (trop simple :P ) mais via un calcul d'aire... Je pose la méthode :

On partage [a;b] en n sous-intervalles par les points a = x(0) < x(1) < x(2) < ... < x(n) = b et on pose D(i) = x(i) - x(i-1).
On choisit, pour chaque i, u(i) appartenant à [x(i-1); x(i)]. Soit A(i) l'aire du ième rectangle : A(i) = D(i) . f(u(i)).
On somme ces aires : E(i=1 jusqu'à n) A(i) = E(i=1 jusqu'à n) D(i).f(u(i)).
On fait tendre n vers +infini avec tous les D(i) tendant vers 0 pour tout i.
Si f est intégrable sur [a;b] alors elle vaut lim(n->+infini) E(i=1 jusqu'à n) D(i).f(u(i)).

Et il faut calculer I(a à b) sin(x) dx.
On suppose évidemment qu'elle est intégrable (pas besoin de tester pour toutes les subdivisions possibles de l'ensemble [a;b]) et la suggestion de l'assistant était de choisir
u(i) = x(i)= a + i . (b-a)/n.

On commence donc par I(a à b) sin(x) dx = lim(n->+infini) E(i=1 jusqu'à n) (b-a)/n . sin(a + i . (b-a)/n)

J'arrive pas trop à commencer, je sais pas comment me débarasser de la somme :(

Merci à tous ceux qui pourront m'aider ^^

[tize]

Je vais essayer de le faire dans un cas simple avec a=0 et b=1, tu pourras facilement compléter la démo pour le cas général :


ensuite, on utilise le fait que est la partie imaginaire de et on calcule :

Donc :

Donc :
ce qu'il fallait démontrer.
Il est facile de voir que le fait de commencer la somme à 0 ou 1 ne change pas le resultat et on peut généraliser le résultat avec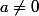 et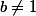
Bon courage