Intégrale abélienne
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lefouineur
- Membre Naturel
- Messages: 68
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 23 Juil 2022, 14:09
par lefouineur » 23 Juil 2022, 14:09
Bonjour à tous,
J'aurai besoin de calculer cette bète là:
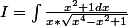
on me conseille d'utiliser le changement de variable: u=x-1/x mais je ne vois pas cette expression en x
apparaitre dans l'intégrale proposée...
Merci de m'aider Cordialement lefouineur
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 23 Juil 2022, 16:26
par Pisigma » 23 Juil 2022, 16:26
Bonjour,
avec l'hypothèse x > 0 tu peux commencer par scinder l'intégrale d'où apparition de simplifications
on me conseille d'utiliser le changement de variable: u=x-1/x le "on" c'est ton prof?
-
lefouineur
- Membre Naturel
- Messages: 68
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 23 Juil 2022, 16:42
par lefouineur » 23 Juil 2022, 16:42
Bonjour Pisigma et merci pour ta réponse rapide,
O.K. pour scinder l'intégrale en deux mais qu'en est-t-il pour le changement de variable?
Je n'ai pas de professeur mais je suis conseillé par mon livre.
Cordialement lefouineur
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 23 Juil 2022, 20:57
par Pisigma » 23 Juil 2022, 20:57
dans ce cas, tu peux utiliser le changement de variable suggéré , calcule
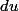
et "arrange toi" pour remplacer les

afin d' avoir uniquement du

sauf erreur de ma part, tu devrais trouver
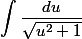
-
lefouineur
- Membre Naturel
- Messages: 68
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 24 Juil 2022, 14:29
par lefouineur » 24 Juil 2022, 14:29
Bonjour Pisigma et merci pour ta réponse,
J'ai eu beau chercher pendant trois heures, je n'ai pas pu me rapprocher de la forme:
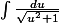
Cela vient probablement du fait que je ne comprends pas ce changement de variable, pourquoi choisir précisément u= x-1/x ? (Voir mon premier message)
Merci de me répondre Cordialement lefouineur
Modifié en dernier par
lefouineur le 24 Juil 2022, 15:55, modifié 1 fois.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 24 Juil 2022, 14:48
par Pisigma » 24 Juil 2022, 14:48
Cela vient probablement du fait que je ne comprends pas ce changement de variable, pourquoi choisir précisément u= x+1/x ? (Voir mon premier message)
attention c'est
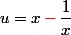
calcule
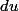
et
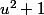
(pourquoi, car ça marche et c'est très rapide pour arriver à la solution ; mais ce n'est pas la seule façon de faire) et ensuite remplace dans
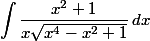
-
lefouineur
- Membre Naturel
- Messages: 68
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 24 Juil 2022, 16:13
par lefouineur » 24 Juil 2022, 16:13
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 24 Juil 2022, 16:35
par Pisigma » 24 Juil 2022, 16:35
sans oublier les parenthèses
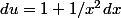
réduis au même dénominateur
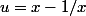
commence par réduire au même dénominateur et élève au carré
ensuite ajoute 1 dans les 2 membres
-
lefouineur
- Membre Naturel
- Messages: 68
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 25 Juil 2022, 11:06
par lefouineur » 25 Juil 2022, 11:06
Bonjour Pisigma et merci pour ta réponse,
Le problème a avancé:
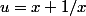
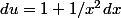
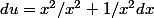
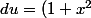/x^2dx)
et
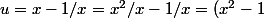/x)
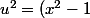^2/x^2)
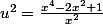
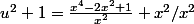
d'oû
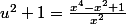
il vient:
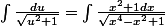
Remarque: il manque x au dénominateur, comment le faire apparaitre?
Cordialement lefouineur
Modifié en dernier par
lefouineur le 25 Juil 2022, 16:05, modifié 1 fois.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 25 Juil 2022, 11:43
par Pisigma » 25 Juil 2022, 11:43
-
lefouineur
- Membre Naturel
- Messages: 68
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 25 Juil 2022, 17:19
par lefouineur » 25 Juil 2022, 17:19
Merci Pisigma pour ta réponse rapide,
J'ai bien compris ton dernier message et je suis arrivé au bout de l'intégrale en distinguant deux cas (signe de x).
Encore merci pour ton aide et ta patience. Cordialement lefouineur
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 25 Juil 2022, 17:22
par Pisigma » 25 Juil 2022, 17:22
je suis arrivé au bout de l'intégrale en distinguant deux cas (signe de x).
que veux-tu dire par là?
-
lefouineur
- Membre Naturel
- Messages: 68
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 25 Juil 2022, 19:59
par lefouineur » 25 Juil 2022, 19:59
Bien y a une primitive pour x>0 et une autre primitive pour x<0
Pourrais-tu me donner une autre méthode pour calculer cette intégrale?
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 25 Juil 2022, 21:12
par Pisigma » 25 Juil 2022, 21:12
Ok
comme déjà dit tu scindes le calcul en 2 parties ( c'est
plus long que la première méthode )
avec
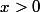
, il vient
\, dx}{x\sqrt{x^4-x^2+1}}\end {aligned})
=
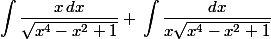
dans la 1ère primitive tu commences par poser
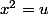
; tu fais apparaître

dans le radicande
ensuite, je te conseille d'utiliser la substitution d'Euler qui dans le cas général où
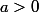
, on pose
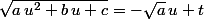
tu peux aussi utiliser les fonctions hyperboliques si tu les connais?
-
lefouineur
- Membre Naturel
- Messages: 68
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 26 Juil 2022, 17:00
par lefouineur » 26 Juil 2022, 17:00
Bonjour Pisigma et merci pour ta réponse rapide,
Mon emploi du temps est fort chargé cette semaine et j'en suis désolé. Je te donne rendez-vous en fin de semaine pour continuer ce topic.
Avec toutes mes excuses Cordialement lefouineur
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 26 Juil 2022, 17:22
par Pisigma » 26 Juil 2022, 17:22
de rien ,"Y a pas l'feu au lac"

-
lefouineur
- Membre Naturel
- Messages: 68
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 09 Aoû 2022, 12:48
par lefouineur » 09 Aoû 2022, 12:48
Bonjour Pisigma,
Dans ton message #14 comment fais-tu pour scinder l'intégrale en deux?
Merci de me répondre cordialement lefouineur
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 09 Aoû 2022, 15:13
par Pisigma » 09 Aoû 2022, 15:13
bin tu as 2 termes au numérateur donc ...
-
lefouineur
- Membre Naturel
- Messages: 68
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 09 Aoû 2022, 17:10
par lefouineur » 09 Aoû 2022, 17:10
Merci Pisigma pour ta réponse rapide,
Pour décomposer l'intégrale en somme de deux intégrales, j'ai pigé:
c'est:
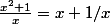
En posant x²=u ,il vient:
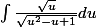
ensuite je ne sais pas: je ne connaissais pas les substitutions d'Euler, j'ai regardé sur Wikipedia
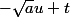
mais que représente t, il n'est pas défini....
Merci pour ton aide cordialement lefouineur
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 10 Aoû 2022, 14:12
par Pisigma » 10 Aoû 2022, 14:12
quand tu poses
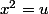
, je n'obtiens pas la même réponse que toi
mais que représente t, il n'est pas défini.... tu dois écrire une relation entre u et t(nouvelle variable)
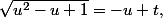
en élevant au carré on obtient

ensuite tu calculeras
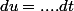
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités