Injectivité et surjectivité

[dragonou]

Bonsoir , si je prends des fonctions simples comme :

f(x) = 2x

f(x) = 2x^2 - 3x + 2

f(x) = ln(3x+1)

comment savoir si elles sont injectives ou surjectives , j'ai pas de bon cours dessus quelqu'un peut m'éclairer ?

merci

[mathelot]

f et g injectives implique gof injective
f et g surjectives implique gof surjective
f injective équivaut à "f admet un inverse à gauche"
f surjective équivaut à "f admet un inverse à droite"

sinon, si f:E F , en restreignant l'ensemble d'arrivée à Im(f),on obtient ainsi une application g: E Im(f) surjective telle que g(x)=f(x).

si f est une application quelconque de E dans F,
on introduit la relation d'équivalence:
xRy ssi f(x)=f(y)
on note E/R l'ensemble quotient et f se décompose selon le diagramme:
E---s--->E/R-----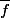---->Im(f)----i----->F
où s est la surjection canonique qui à x associe sa classe d'équivalence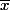 , 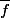est une bijection et i l'injection canonique
qui est l'inclusion de Im(f) dans F.

[mathelot]

f(x) = 2x

f(x) = 2x^2 - 3x + 2

f(x) = ln(3x+1)

comment savoir si elles sont injectives ou surjectives , j'ai pas de bon cours dessus quelqu'un peut m'éclairer ?

merci

application:
x--->2x est bijectif de R sur R. En effet, pour tout y de R,
l'équation d'inconnue x , y=2x a une unique solution.

x ----> f(x) = 2x^2 - 3x + 2
n'est ni injective , ni surjective.
Il suffit d'écrire f sous sa forme canonique:
f(x)=2[(x-3/4)^2-5/4]
on "voit" ainsi qu'il faut restreindre l'ensemble d'arrivée à [-5/4;+oo[
pour que f soit surjective.
Il faut restreindre l'ensemble de départ de f à [3/4;+oo[
ou alors à ]-oo;3/4] pour que f soit injective.

x--->f(x) = ln(3x+1)
L'ensemble de départ est au maximum ]-1/3;+oo[
composée de 2 injections donc injective.
Elle est surjective sur R comme arrivée.

[dragonou]

merci mathelot mais j'ai quelques interrogations s'il te plait car tu as été très formel lol :

1.quand une fonction est bijective elle ne peut pas etre injective ou subjective si je lis çà :

application:
x--->2x est bijectif de R sur R. En effet, pour tout y de R,
l'équation d'inconnue x , y=2x a une unique solution.

2.x ----> f(x) = 2x^2 - 3x + 2
n'est ni injective , ni surjective.
Il suffit d'écrire f sous sa forme canonique:
f(x)=2[(x-3/4)^2-5/4]
on "voit" ainsi qu'il faut restreindre l'ensemble d'arrivée à [-5/4;+oo[
pour que f soit surjective.

La forme canonique tu veux dire a(x-x1)(x-x2,)?
Ensuite , c'est quoi cet ensemble d'arrivée et l'ensemble de départ ?

3.x--->f(x) = ln(3x+1)
L'ensemble de départ est au maximum ]-1/3;+oo[
composée de 2 injections donc injective.
Elle est surjective sur R comme arrivée.

C'est le domaine de définition -1/3 + inf , donc c'est quoi l'ensemble de départ ?

Ensuite , tu écris :

si f est une application quelconque de E dans F

Mais que représente E et F , tu es trop formel c'est flou , peux tu donner des précisions stp .

Je ne comprends pas concrètement ce que c'est une fonction unjective ou subjective...

merci

[fahr451]

injective : tout élément de l'ensemble d'arrivée a au plus un antécédent.
surjective : tout élément de l'ensembled'arrivéé a au moins un antécédent.

bijective = injective et surjective c'est à dire
tout élément de l 'ensemble d 'arrivée a exactement un antécédent.