Injectivité et surjectivité

[Prog4ever]

Bonjour,

J'ai un problème à résoudre et je ne sais tout simplement pas comment y arriver... Voici l'énoncé:

Considérons la fonction f : Q^2;) Q^2 définie par :
f(x, y) = (x + y, x ;) y)
a) La fonction f est-elle injective, surjective, bijective ? Justifiez vos r ;)eponses.
b) Si f est bijective, donnez son inverse. Donnez le calcul explicite de f;)1;)f.

Comment fait-on pour savoir si elle est injective, bijective ou surjective..?

Merci de votre aide!

[Matt_01]

Que veut dire injectif, surjectif, bijectif ?
Applique les définitions et montre nous où tu as des difficultés.

[Prog4ever]

Que veut dire injectif, surjectif, bijectif ?
Applique les définitions et montre nous où tu as des difficultés.

Voici les définitions (si je ne me trompe...):

Injectif : pour tous éléments du premier ensemble on trouve un seul élément distinct dans le deuxième ensemble

Surjectif: pour tous éléments du 2e ensemble, il y a AU MOINS un élément du premier ensemble

Bijectif: à la fois injectif et surjectif.

Je ne comprends tout simplement pas comment démontrer si c'est l'un ou l'autre...
(On parle du domaine de mathématiques pour informaticien/mathématiques discrètes)

[Matt_01]

Revois tes définitions (et essaye de les comprendre), car ce que tu as écrit ne veut rien dire.

[Anonyme]

@Prog4ever

Comme Q muni de le loi + est un groupe , f est bien une fonction de Q^2 dans Q^2
(en fait c'est une application Q^2 dans Q^2 )

1) Injectivité
La fonction f est injective si et seulement si et

si alors


2) Surjectivité
La fonction f est surjective si et seulement si
et tel que

Il faut donc vérifier si ces 2 propriétés sont vraies ?

Question :
Que veut dire qu'une fonction est bijective ?
et est-ce que la fonction f est bijective ?

[Kikoo <3 Bieber]

Salut,

Dans l'énoncé, quand on parle d'inverse, ne s'agirait-il pas plutôt de bijection réciproque ?

[Anonyme]

est la notation de la fonction réciproque de la fonction f

[Prog4ever]

@Prog4ever

Comme Q muni de le loi + est un groupe , f est bien une fonction de Q^2 dans Q^2
(en fait c'est une application Q^2 dans Q^2 )

1) Injectivité
La fonction f est injective si et seulement si et

si alors


2) Surjectivité
La fonction f est surjective si et seulement si
et tel que

Il faut donc vérifier si ces 2 propriétés sont vraies ?

Question :
Que veut dire qu'une fonction est bijective ?
et est-ce que la fonction f est bijective ?

Oui en effet il faut vérifier les deux, mais comment prouver une telle chose?

[Anonyme]

@Prog4ever

en écrivant 2 "raisonnements"

[Prog4ever]

@ptitnoir

Pourrais-je avoir une piste de raisonnement svp..? Je ne sais par où commencer.

[Matt_01]

Salut,

Dans l'énoncé, quand on parle d'inverse, ne s'agirait-il pas plutôt de bijection réciproque ?

L'ensemble des fonctions bijectives de E dans E forme un groupe pour la composition, appelé groupe symétrique. On peut donc parler d'inverse (pour donc l'opération de composition).

[Anonyme]

@Prog4ever

Pour l'injectivité

1) commence par écrire ce que veut dire

2) puis essaie de "voir" si cela implique que

[Anonyme]

Comme les fonctions bijectives d'un ensemble E sur lui même muni de la loi composition ° est un groupe

la fonction notée est la fonction "inverse" de la fonction pour la loi °

Et on dit fonction réciproque et non pas fonction "inverse"
"même si c'est vrai"


et on a : ° = ° =

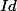
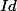étant la fonction bijective telle que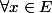
(élément neutre du groupe)

[Anonyme]

@Kikoo <3 Bieber

Es tu au courant que la notation existe également pour des fonctions non bijectives ?

[Judoboy]

Bieber : c'est pas plutôt 8 minutes ton daily fact ?