Bonsoir, pourriez-vous m'aider à cet exercice s'il vous plaît ?
Soient L,J deux intervalles, f:L→J une fonction bijective, et soit g:J→L sa réciproque. Composez une démonstration de l'injectivité de g en choisissant des phrases données plus bas.
Soient ..... tels que ....... Il faut montrer ......
-t2 a une image
- t1 ≠ t2
- t1 a un antécédent
- f(t1)=f(t2)
- g(t2)=t1
- t1, t2 ∈ J
- t1 = t2
- f(t1)=t2
- g(t1)=g(t2)
- t1 ∈ L, t2 ∈ J
- g(t1) ≠ g(t2)
- t1, t2 ∈ L
Injectivité réciproque
11 messages
- Page 1 sur 1
Re: Injectivité réciproque
Connais tu la définition d'une fonction injective? Si oui tu devrais savoir remplir les pointillés facilement.
Re: Injectivité réciproque
Bonsoir,
Ça commence forcément par : "Soient t1 et t2 dans J", parce qu'ils appartiennent forcément au même ensemble de points (J ou L) (car on ne parle pas d'unicité), et qu'il n'y a pas de bout de phrase où on parle de leurs antécédents par g.
Après c'est "tels que t1 ≠ t2" ou c'est "tels que g(t1)=g(t2)".
Ça commence forcément par : "Soient t1 et t2 dans J", parce qu'ils appartiennent forcément au même ensemble de points (J ou L) (car on ne parle pas d'unicité), et qu'il n'y a pas de bout de phrase où on parle de leurs antécédents par g.
Après c'est "tels que t1 ≠ t2" ou c'est "tels que g(t1)=g(t2)".
Re: Injectivité réciproque
Salut,
Oui, car avec une fonction injective : chaque image de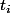 , si elle existe, est unique. Il n'existe pas deux point de l'abscisse à la même ordonnée. Donc en prouvant que si deux points de l'axe horizontal possèdent la même coordonnée verticale; il sont égaux, tu démontres que la fonction est injective.
, si elle existe, est unique. Il n'existe pas deux point de l'abscisse à la même ordonnée. Donc en prouvant que si deux points de l'axe horizontal possèdent la même coordonnée verticale; il sont égaux, tu démontres que la fonction est injective.
Cordialement.
Oui, car avec une fonction injective : chaque image de
Cordialement.
Re: Injectivité réciproque
Merci ! Cependant je ne sais pas comment continuer, je dois ensuite choisir quatre phrases entre :
- Comme f est injective, f(g(s1))=f(g(s2)).
- Grâce à l'injectivité de f j'ai s1=g(f(s 1)) et s2=g(f(s 2)).
- J'en déduis s1=f(g(s1))=f(g(s2))=s2.
- Comme f est une fonction, f(g(s1))=f(g(s2)).
- Par définition de fonction réciproque s1=g(f(s1)) et s2=g(f(s2)).
- Donc s 1=g(f(s1))=g(f(s2))=s2.
- Puisque f est bijective, s1=f(g(s1)) et s2=f(g(s2)).
et les mettre bout à bout à la suite.
- Comme f est injective, f(g(s1))=f(g(s2)).
- Grâce à l'injectivité de f j'ai s1=g(f(s 1)) et s2=g(f(s 2)).
- J'en déduis s1=f(g(s1))=f(g(s2))=s2.
- Comme f est une fonction, f(g(s1))=f(g(s2)).
- Par définition de fonction réciproque s1=g(f(s1)) et s2=g(f(s2)).
- Donc s 1=g(f(s1))=g(f(s2))=s2.
- Puisque f est bijective, s1=f(g(s1)) et s2=f(g(s2)).
et les mettre bout à bout à la suite.
Re: Injectivité réciproque
Il faut donc supposer que c'est la phrase g(s1)=g(s2) qu'il fallait choisir (avec des t qui sont devenus des s ).
Pour prouver l'injectivité de g, il faut montrer que s1=s2, en utilisant f bien entendu. Quelle est la définition d'une fonction réciproque (regarde dans ton cours) ?
Je te conseille de le démontrer sans regarder les phrases.... puis une fois démontré de recoller les morceaux.
Pour prouver l'injectivité de g, il faut montrer que s1=s2, en utilisant f bien entendu. Quelle est la définition d'une fonction réciproque (regarde dans ton cours) ?
Je te conseille de le démontrer sans regarder les phrases.... puis une fois démontré de recoller les morceaux.
Re: Injectivité réciproque
cet énoncé est une catastrophe pédagogique. au lieu de travailler sur le sens, on travaille sur la syntaxe 

Modifié en dernier par mathelot le 13 Oct 2017, 18:19, modifié 1 fois.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
