Inégalité de Cauchy-schwarz
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Orph123
- Membre Naturel
- Messages: 39
- Enregistré le: 21 Fév 2021, 09:32
-
 par Orph123 » 07 Oct 2021, 06:11
par Orph123 » 07 Oct 2021, 06:11
Bonjour tout le monde.
Svp je voudrais avoir seulement une indication pour la partie suivante d'un exercice qui traite l'inégalité de Cauchy-schwarz dans la sommations des réels.
"Soient (a1,a2,...,an) des réels strictement positifs, et (b1,b2,...,bn) des réels. On suppose an<...<a2<a1 et que pour tout k de {1,2,...,n}:

MONTRER QUE:
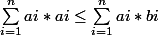
"
Modifié en dernier par
Orph123 le 08 Oct 2021, 11:32, modifié 1 fois.
-
Orph123
- Membre Naturel
- Messages: 39
- Enregistré le: 21 Fév 2021, 09:32
-
 par Orph123 » 07 Oct 2021, 20:55
par Orph123 » 07 Oct 2021, 20:55
Svp j ai besoin d un indice j arrive pas du tt à avancer dans la qst!!!!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 08 Oct 2021, 11:14
par Ben314 » 08 Oct 2021, 11:14
Je comprend vraiment pas ce que tu fait avec tes sommes à rallonges (pourquoi faire simple quand on peut faire compliqué . . . ) :
+a_3(B_3\!-\!B_2)+...+a_n(B_n\!-\!B_{n-1})\cr<br />\ \ \ =(a_1\!-\!a_2)B_1+(a_2\!-\!a_3)B_2+...+\!(a_{n-1}\!-\!a_n)B_{n-1}+a_nB_n\cr<br />\ \ \ \geq(a_1\!-\!a_2)A_1+(a_2\!-\!a_3)A_2+...+\!(a_{n-1}\!-\!a_n)A_{n-1}+a_nA_n)
Vu que
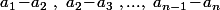
et

sont >0 et que
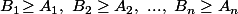
Et on termine en écrivant que le minorant trouvé est
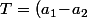A_1+(a_2\!-\!a_3)A_2+...+\!(a_{n-1}\!-\!a_n)A_{n-1}+a_nA_n\cr<br />\ \ \ =a_1A_1+a_2(A_2\!-\!A_1)+a_3(A_3\!-\!A_2)+...+a_n(A_n\!-\!A_{n-1})\cr<br />\ \ \ =a_1a_1+a_2a_2+...+a_na_n)
Modifié en dernier par
Ben314 le 09 Oct 2021, 00:03, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Orph123
- Membre Naturel
- Messages: 39
- Enregistré le: 21 Fév 2021, 09:32
-
 par Orph123 » 08 Oct 2021, 15:24
par Orph123 » 08 Oct 2021, 15:24
Merci pour votre indication.
Donc là j'ai essayer de trouver justement une relation entre Bl et les bk du coup j'ai calculer (Bl+Al)² et j'ai trouver la somme de plusieurs sommes et ça devient très compliqué.
Qu'est ce que vous proposez comme reponse à cette qst vous parce que là je pense que j'ai vrmt tt essayer


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 08 Oct 2021, 16:53
par Ben314 » 08 Oct 2021, 16:53
Orph123 a écrit:Merci pour votre indication.
Donc là j'ai essayer de trouver justement une relation entre Bl et les bk du coup j'ai calculer (Bl+Al)² et . . .
Je vois pas le rapport qu'il peut y avoir entre ce que je t'ai incité à faire, à savoir d'exprimer les
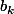
en fonction des
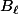
et le fait de calculer (Bl+Al)^2.
Bref, revenons à du basique : si on te dit que
B1=3 (=b1)
B2=7 (=b1+b2)
B3=11 (=b1+b2+b3)
B4=12 (=b1+b2+b3+b4)
B5=17 (=b1+b2+b3+b4+b5)
est-tu capable ou pas de retrouver les valeurs de b1,b2,b3,b4 et b5 ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 08 Oct 2021, 17:22
par GaBuZoMeu » 08 Oct 2021, 17:22
Bonjour,
Si je peux me permettre, une autre (?) piste :
Soit

le vecteur de coordonnées
)
,

celui de coordonnées
)
. On a à démontrer
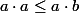
, c.-à-d.
 \geq 0)
.
Que sait-on ? On sait que
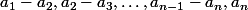
sont tous strictement positifs. On sait aussi que
+(b_2-a_2),\ldots \sum_{i=1}^n(b_i-a_i))
sont tous positifs ou nuls. On aurait envie de dire que les premiers sont les coordonnées de

dans une base, les seconds les coordonnées de
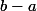
dans une autre base et ... que le produit scalaire donne une relation sympa entre ces deux bases.
-
Orph123
- Membre Naturel
- Messages: 39
- Enregistré le: 21 Fév 2021, 09:32
-
 par Orph123 » 08 Oct 2021, 19:54
par Orph123 » 08 Oct 2021, 19:54
Ben314 a écrit: Orph123 a écrit:Merci pour votre indication.
Donc là j'ai essayer de trouver justement une relation entre Bl et les bk du coup j'ai calculer (Bl+Al)² et . . .
Je vois pas le rapport qu'il peut y avoir entre ce que je t'ai incité à faire, à savoir d'exprimer les
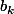
en fonction des
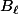
et le fait de calculer (Bl+Al)^2.
Bref, revenons à du basique : si on te dit que
B1=3 (=b1)
B2=7 (=b1+b2)
B3=11 (=b1+b2+b3)
B4=12 (=b1+b2+b3+b4)
B5=17 (=b1+b2+b3+b4+b5)
est-tu capable ou pas de retrouver les valeurs de b1,b2,b3,b4 et b5 ?
Donc si je pars de cette idée là j ai trouvé ceci:
(Vous le trouverez svp dzns ce lien par ce que ça donne des sommes un peu compliquées à ecrire:
https://www.camscanner.com/share/show?encrypt_id=MHhkYmM2MGY2MQ%3D%3D&sid=F415C60BBB6F4607TR79X7YfUS&pid=dsa&style=1Et puis je trouve une somme double et j interchange les indices, et là je me bloque encore

-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 08 Oct 2021, 21:06
par GaBuZoMeu » 08 Oct 2021, 21:06
La piste que je t'ai suggéré ne nécessite pas beaucoup de calculs.
-
Orph123
- Membre Naturel
- Messages: 39
- Enregistré le: 21 Fév 2021, 09:32
-
 par Orph123 » 08 Oct 2021, 21:14
par Orph123 » 08 Oct 2021, 21:14
GaBuZoMeu a écrit:La piste que je t'ai suggéré ne nécessite pas beaucoup de calculs.
Oui j'ai lu votre réponse mais je ne maîtrise pas trop la notions de vecteurs en mathématiques pour pouvoir bien comprendre votre démonstration.
Par ailleurs si on veut procéder par calcul sur des réels que me suggèrez vous pour la fin de ma réponse ??? Je vous remercie énormément pour votre collaboration et aide!!
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 08 Oct 2021, 21:22
par GaBuZoMeu » 08 Oct 2021, 21:22
Désolé, j'ai un peu la flemme de plonger dans les calculs. Je laisse Ben314.
-
Orph123
- Membre Naturel
- Messages: 39
- Enregistré le: 21 Fév 2021, 09:32
-
 par Orph123 » 08 Oct 2021, 21:24
par Orph123 » 08 Oct 2021, 21:24
Pas de soucis je vous remercie pour votre aide!!


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Oct 2021, 00:04
par Ben314 » 09 Oct 2021, 00:04
Je comprend vraiment pas ce que tu fait avec tes sommes à rallonges
(pourquoi faire simple quand on peut faire compliqué . . . ) :
+a_3(B_3\!-\!B_2)+...+a_n(B_n\!-\!B_{n-1})\cr<br />\ \ \ =(a_1\!-\!a_2)B_1+(a_2\!-\!a_3)B_2+...+\!(a_{n-1}\!-\!a_n)B_{n-1}+a_nB_n\cr<br />\ \ \ \geq(a_1\!-\!a_2)A_1+(a_2\!-\!a_3)A_2+...+\!(a_{n-1}\!-\!a_n)A_{n-1}+a_nA_n)
Vu que
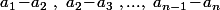
et

sont >0 et que
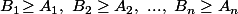
Et on termine en écrivant que le minorant trouvé est
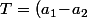A_1+(a_2\!-\!a_3)A_2+...+\!(a_{n-1}\!-\!a_n)A_{n-1}+a_nA_n\cr<br />\ \ \ =a_1A_1+a_2(A_2\!-\!A_1)+a_3(A_3\!-\!A_2)+...+a_n(A_n\!-\!A_{n-1})\cr<br />\ \ \ =a_1a_1+a_2a_2+...+a_na_n)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Orph123
- Membre Naturel
- Messages: 39
- Enregistré le: 21 Fév 2021, 09:32
-
 par Orph123 » 09 Oct 2021, 02:46
par Orph123 » 09 Oct 2021, 02:46
En fait là faudra vraiment que je revoie ma méthode de travail parce que je suppose toujours que le truc sera très compliqué du coup je pars toujours de l'idée que cette question sera difficile donc sa réponse serait compliquée et je comprends plus ça m'arrive toujours et surtout en maths, la réponse est assez simple et si tu regardes mon raisonnement tu trouveras des choses assez compliquées et au final sans même pouvoir y répondre!! :"( Pouvez-vous Monsieur me donner quelques conseils pour avoir une logique de résolution plus rigoureuse et comment je pourrais savoir simplifier tout mon calcul avant d'entamer la question ? Est-ce que je devrais peut-être avoir dès le début avant de commencer à rédiger mon raisonnement avoir en tête qu'est ce qu'on veut et qu'est ce qu'on a pour cela?
Et je tiens finalement à vous remercier de tout mon cœur pour votre travail et aide assez distingués!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités

