Inégalité de Bessel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
yggdrasiil
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Nov 2006, 15:25
-
 par yggdrasiil » 14 Jan 2007, 21:36
par yggdrasiil » 14 Jan 2007, 21:36
Soit E un espace vectoriel muni d'un produit scalaire. Si {
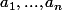
} sont des vecteurs orthogonaux non nuls dans E, montrer l'inégalité de Bessel :
}{||a_{i}||^{2}}\leq ||x||^{2})
Je n'avais jamais vu l'inégalité de Bessel, en tout cas pas sous cette forme.
Comment commencer ?
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
 par jose_latino » 14 Jan 2007, 22:09
par jose_latino » 14 Jan 2007, 22:09
C'est vraiment
|^2}{||a_{i}||^{2}} \leq ||x||^{2})
-
jose_latino
- Membre Relatif
- Messages: 320
- Enregistré le: 25 Juil 2006, 21:09
-
 par jose_latino » 14 Jan 2007, 22:18
par jose_latino » 14 Jan 2007, 22:18
Tu peux utiliser un fait intéressant: La projection orthogonale

de

sur le sous espace

engrendré par
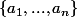
accomplit que
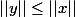
(*). Justement, le carré de la norme de

est le coté gauche de l'inégalité de Bessel. La formule de la projection tu peux l'obtenir en utilisant que
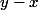
est orthogonal à

et
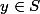
, en conséquence
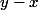
est orthogonal à tous les éléments de
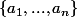
et je peux exprimer à

comme combinason linéaire de
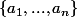
. Pour obtenir (*), utilise le théorème de Pythagoras pour

et
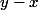
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 14 Jan 2007, 22:37
par fahr451 » 14 Jan 2007, 22:37
en effet en supposant les ai de norme 1 (ce qui allège l 'écriture)
(a1,...,an) est une base orthonormée de F = vect (a1,...,an)
la projection orthogonale de x sur f est y définie par
y = sigma (xlai)ai sa norme au carré est sigma (xlai)^2
et x = x-y +y or x-y et y sont orthogonaux donc pythagore permet de conclure
REM il manque un carré dans ton inégalité
-
yggdrasiil
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Nov 2006, 15:25
-
 par yggdrasiil » 14 Jan 2007, 23:00
par yggdrasiil » 14 Jan 2007, 23:00
Merci de vos réponses, je vais essayer de me débrouiller avec ça.
fahr451 a écrit:REM il manque un carré dans ton inégalité
Hum ? Elle manque donc aussi sur la feuille de données des exercices. J'ai voué une confiance aveugle à mon prof ma foi...
-
yggdrasiil
- Membre Naturel
- Messages: 50
- Enregistré le: 09 Nov 2006, 15:25
-
 par yggdrasiil » 14 Jan 2007, 23:57
par yggdrasiil » 14 Jan 2007, 23:57
Pourquoi a-t-on :
fahr451 a écrit:y = sigma (xlai)ai sa norme au carré est sigma (xlai)^2
et x = x-y +y or x-y et y sont orthogonaux
?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités