Indépendance linéaire

[Marcet003]

Bonjour,

J'aimerais montrer que la famille de vecteur est linéairement indépendante sur . Je pose donc : .

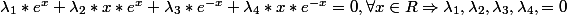
En dérivant successivement l'expression ci-dessus 4 fois, dont les dérivées sont identiquement nulles et en évaluant chaque fois en zéro j'obtiens 4eq. qui me permettent de verifier in fine que la famille est libre.
Y a-t-il un moyen plus rapide ?
Merci d'avance...

[Ben314]

Salut,
Personnellement j'aurais utilisé le fait que les 4 fonctions n'ont pas le même type de croissance en , plus précisément j'aurais (dans cet ordre) :
1) Multiplié par puis fait tendre vers
2) Multiplié par puis fait tendre vers
3) Multiplié par puis fait tendre vers
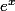
4) Multiplié par puis fait tendre vers

Et si tu as vu la notion d'équivalent (de fonctions), ça revient à dire que, si un des coeff. est non nul, alors ta fonction va avoir un équivalent (non nul) en .

[Marcet003]

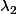
Si j'ai bien compris l'histoire d'équivalent. Par exemple en reprenant , dans le cas où ce coeff. est non nul et en notant la fonction tirée de l'équation. On a :


Ce qui pose problème avec le fait que on a posé ?

En tt. cas merci du truc, c'est bien plus rapide...