Indépendance linéaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par optimistik-moi » 27 Nov 2008, 21:01
par optimistik-moi » 27 Nov 2008, 21:01
Bonsoir,
je cherche à savoir si la famille (x->e^ax) avec a élément des réels est une famille linéairement indépendante ou pas . comment faire?
merci d'avance.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 27 Nov 2008, 22:57
par skilveg » 27 Nov 2008, 22:57
Tu peux par exemple faire une étude asymptotique, ou encore utiliser un déterminant de Vandermonde, je crois.
Bonne soirée
-
seriousme
- Membre Relatif
- Messages: 122
- Enregistré le: 26 Fév 2007, 13:10
-
 par seriousme » 27 Nov 2008, 23:11
par seriousme » 27 Nov 2008, 23:11
Il faut montrer que toute combinaison linéaire nulle a tous ses coefficients nuls.
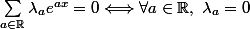
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 27 Nov 2008, 23:27
par ffpower » 27 Nov 2008, 23:27
seriousme a écrit:Il faut montrer que toute combinaison linéaire nulle a tous ses coefficients nuls.
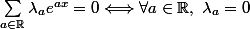
Pas tout a fait.faut supposer la somme finie...
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 28 Nov 2008, 00:45
par Luc » 28 Nov 2008, 00:45
Bonsoir,
Regarde les limites en
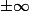
. Ca te permet presque d'arriver au résultat.
PS: n'oublie pas de regarder en 0 aussi, sinon tu oublies un cas...
Luc
-
seriousme
- Membre Relatif
- Messages: 122
- Enregistré le: 26 Fév 2007, 13:10
-
 par seriousme » 28 Nov 2008, 00:47
par seriousme » 28 Nov 2008, 00:47
En effet c'est plus rigoureux.
Mais, concrètement, en quoi une somme infinie pourrait poser problème dans ce cas et/ou pour une autre famille infinie ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Nov 2008, 12:08
par leon1789 » 28 Nov 2008, 12:08
seriousme a écrit:En effet c'est plus rigoureux.
Mais, concrètement, en quoi une somme infinie pourrait poser problème dans ce cas et/ou pour une autre famille infinie ?
Une somme infinie, c'est tout simplement contraire à la définition d'une combinaison linéaire !
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 28 Nov 2008, 12:14
par ffpower » 28 Nov 2008, 12:14
Cela dit ici,ca marcherait qd meme mais c est pas la définition.On pourrait meme allait plus loin:Si

est une mesure signée sur R telle que pour tout x,
=0)
alors
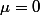

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Nov 2008, 12:26
par leon1789 » 28 Nov 2008, 12:26
ffpower a écrit:Cela dit ici,ca marcherait qd meme mais c est pas la définition.
une somme (discrète) indexée sur N, ok, j'imagine... mais sur R ?!
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 29 Nov 2008, 11:44
par skilveg » 29 Nov 2008, 11:44
Je me permets de revenir sur ce que je disais, qui me parait une solution un peu plus jolie que l'étude asymptotique: si on a une relation de liaison, on la dérive

fois, et on obtient un vecteur du noyau d'une matrice de Vandermonde inversible, qui est donc nul: les coefficients de la relation de liaison sont donc nuls.
Cordialement
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
 fois, et on obtient un vecteur du noyau d'une matrice de Vandermonde inversible, qui est donc nul: les coefficients de la relation de liaison sont donc nuls.
fois, et on obtient un vecteur du noyau d'une matrice de Vandermonde inversible, qui est donc nul: les coefficients de la relation de liaison sont donc nuls.