Salut,
Si c'est cette égalité :
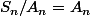
que tu ne comprend pas, ben c'est on ne peut plus normal vu que c'est non seulement faux, mais aussi parfaitement incohérent : les élément de
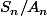
c'est des classes modulo

, c'est à dire des parties de

et ça risque pas d'être la même chose que des éléments de

.
Et d'un autre coté, je comprend pas franchement l'intérêt de la preuve en question. La façon dont on procède pour calculer le cardinal de

dépend bien évidement de la façon dont on l'a défini (et il y a évidement pas mal de définitions possibles).
Ici, vu le laïus, ça donne l'impression qu'il est défini comme étant l'ensemble des permutations de signatures =+1. Et si la notion de signature est déjà connue, ben en général ça signifie qu'on sait aussi que la fonction "signature" est un morphisme de groupe surjectif de (Sn,o) sur ({-1,+1},x) ce qui signifie que

c'est le noyau de cette fonction signature et à peu prés tout est dit.


