Image d'un cercle par app complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 22 Juin 2015, 09:44
par adamNIDO » 22 Juin 2015, 09:44
Bonjour,
quelle est la methode generale pour resoudre ce type de question

merci
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 22 Juin 2015, 10:13
par paquito » 22 Juin 2015, 10:13
adamNIDO a écrit:Bonjour,
quelle est la methode generale pour resoudre ce type de question

merci
tu peux procéder par élimination.
Exemple: A le cercle passerait par A; tu résous i=z' et tu regarde si ça marche.
Ou chercher l'image de |z-i|=1.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 22 Juin 2015, 10:39
par arnaud32 » 22 Juin 2015, 10:39
le cercle de centre aA et de rayon 1 a pour equation |z-i|=1 ...
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 22 Juin 2015, 11:29
par paquito » 22 Juin 2015, 11:29
arnaud32 a écrit:le cercle de centre aA et de rayon 1 a pour equation |z-i|=1 ...
Résultat basique!
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 22 Juin 2015, 11:59
par adamNIDO » 22 Juin 2015, 11:59
merci mais j'ai pas bien compris le procedure et l'objective svp si quelqu'un peut m'expliquer ou bien existe t il un pdf contient exemple concrete
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 22 Juin 2015, 12:14
par arnaud32 » 22 Juin 2015, 12:14
ca veut dire que

et donc
}}{2})
-
mathelot
 par mathelot » 22 Juin 2015, 12:20
par mathelot » 22 Juin 2015, 12:20
adamNIDO a écrit:merci mais j'ai pas bien compris le procedure et l'objective svp si quelqu'un peut m'expliquer ou bien existe t il un pdf contient exemple concrete
bonjour,

i})
l'image du cercle C(A,1) est le cercle de centre O et de rayon 1/2
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 22 Juin 2015, 18:08
par adamNIDO » 22 Juin 2015, 18:08
mathelot a écrit:bonjour,

i})
l'image du cercle C(A,1) est le cercle de centre O et de rayon 1/2
bonjour veuillez me detailler les choses etape par etape:
dabord qui est ce qu'on a :
=z'=\frac{i}{2(z-i)})
on chercher T(C(A,1))=? avec A(z) alors comment on va procede etape par etape svp
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 22 Juin 2015, 19:37
par adamNIDO » 22 Juin 2015, 19:37
svp votre aide
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 22 Juin 2015, 20:02
par adamNIDO » 22 Juin 2015, 20:02
mathelot a écrit:bonjour,

i})
l'image du cercle C(A,1) est le cercle de centre O et de rayon 1/2
merci mais je vois pas pk
i})
equivalent a une cercle de centre 0 et de rayon 1/2 svp une deifntion de cercle dans le cadre complexe a part |z-omega|=r
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 22 Juin 2015, 22:30
par adamNIDO » 22 Juin 2015, 22:30
voila ce que je comprend:
M(z):designe que z affixe de point M
 \in \mathcal{C}(A(i),1) \Longleftrightarrow |z-i|=1\\<br /> |z-i|=1\Longleftrightarrow |z-i|=|e^{i\theta}|\\<br />\Longleftrightarrow z-i=e^{i\theta}\\<br />\Longleftrightarrow z=i+e^{i\theta})
alors limage de
,1))=T(z=i+e^{i\theta})=\dfrac{i}{2((i+e^{i\theta})-i)}=<br />\dfrac{i}{2(e^{i\theta})}=\dfrac{e^{\frac{\pi}{2}}}{2(e^{i\theta})}=\dfrac{1}{2}e^{\frac{\pi}{2}-\theta})
finalement
,1))=\dfrac{1}{2}e^{\pi/2-\theta})
je sais pas comment interpreter cette expression

comme cercle je sais seulement la defintion d'un cercle :
rappel: \in \mathcal{C}(A(i),1) \Longleftrightarrow |z-i|=1)
merci et j'espere que quelqu'un me comprendre
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Juin 2015, 03:36
par adamNIDO » 23 Juin 2015, 03:36
Bonjour,
est ce que cela est vrai
 \in \mathcal{C}(A(h),r) \Longleftrightarrow |z-h|=r \Longleftrightarrow |z-h|=|re^{i\theta}| \quad \forall \theta \in \mathbb{R}\Longleftrightarrow z=h+re^{i\theta} \quad \forall \theta \in \mathbb{R})
-
mathelot
 par mathelot » 23 Juin 2015, 07:41
par mathelot » 23 Juin 2015, 07:41
adamNIDO a écrit:alors limage de
,1))=T(z=i+e^{i\theta})=\dfrac{i}{2((i+e^{i\theta})-i)}=<br />\dfrac{i}{2(e^{i\theta})}=\dfrac{e^{i\frac{\pi}{2}}}{2(e^{i\theta})}=\dfrac{1}{2}e^{i(\frac{\pi}{2}-\theta)})
avec les modules
}|=\frac{|i|}{2|z-i|}=\frac{1}{2 \times 1}=\frac{1}{2})
donc
) \subset C'(0,\frac{1}{2}))
pour la réciproque

donc
 \subset T(C(i,1)))
de plus, l'application

est une surjection de

sur le disque unité
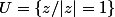
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Juin 2015, 08:31
par adamNIDO » 23 Juin 2015, 08:31
mathelot a écrit:avec les modules
}|=\frac{|i|}{2|z-i|}=\frac{1}{2 \times 1}=\frac{1}{2})
donc
) \subset C'(0,\frac{1}{2}))
pour la réciproque

donc
 \subset T(C(i,1)))
de plus, l'application

est une surjection de

sur le disque unité
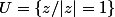
Bonjour,
merci pour votre aide mais :
est ce que ce qui j'ai ecrit est vraie ?
concernant votre methode si je veux faire la redaction de solution sera comme ca :
Soit
 \in T(C(i,1)))
et on montrons que
\in C'(0,\frac{1}{2}))
en effet,
 \in T(C(i,1)) \Longleftrightarrow |z'|=|\frac{i}{2(z-i)}|=\frac{|i|}{2|z-i|}=\frac{1}{2 \times 1}=\frac{1}{2} \Longleftrightarrow |z'|=1 \Longleftrightarrow M(z)\in C'(0,\frac{1}{2})) dans l'autre sense
dans l'autre sense \in C'(0,\frac{1}{2}) \Longleftrightarrow |z-i|=|\frac{i}{2z'}|=1 \Longleftrightarrow |z-i |=1 \Longleftrightarrow M(z) \in T(C(i,1)))
donc
 \subset T(C(i,1)))
SVP A quoi va nous servir que l'application

est une surjection de

sur le disque unité
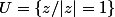
merci pour votre aide
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Juin 2015, 08:39
par adamNIDO » 23 Juin 2015, 08:39
Concernant la methode que j'ai utilise est ce qu'elle est bien :
Soit M(z): designe que le point M d'affixe z
 \in \mathcal{C}(A(i),1) \Longleftrightarrow |z-i|=1\\<br /> |z-i|=1\Longleftrightarrow |z-i|=|e^{i\theta}|\\<br />\Longleftrightarrow z-i=e^{i\theta}\\<br />\Longleftrightarrow z=i+e^{i\theta})
On cherche limage de
,1)))
en effet,
 \in T( \mathcal{C}(A(i),1)) \Longleftrightarrow T(z)=\dfrac{i}{2((i+e^{i\theta})-i)}=<br />\dfrac{i}{2(e^{i\theta})}=\dfrac{e^{\frac{\pi}{2}}}{2(e^{i\theta})}=\dfrac{1}{2}e^{\frac{\pi}{2}-\theta})
finalement
 \in T( \mathcal{C}(A(i),1)) \Longleftrightarrow T(z)=\dfrac{1}{2}e^{\pi/2-\theta})
mais je sais pas comment linterpréter comme une cercle cest parce que j'ai ecrit que
 \in \mathcal{C}(A(h),r) \Longleftrightarrow |z-h|=r \Longleftrightarrow |z-h|=|re^{i\theta}| \quad \text{ avec } \theta \in \mathbb{R}\Longleftrightarrow z=h+re^{i\theta} \quad \text{ avec } \theta \in \mathbb{R})
merci pour votre aide
-
mathelot
 par mathelot » 23 Juin 2015, 08:39
par mathelot » 23 Juin 2015, 08:39
adamNIDO a écrit:SVP A quoi va nous servir que l'application

est une surjection de

sur le disque unité
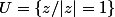
c'est pour avoir une caractérisation du cercle comme courbe paramétrée par une exponentielle
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Juin 2015, 08:40
par adamNIDO » 23 Juin 2015, 08:40
mathelot a écrit:c'est pour avoir une caractérisation du cercle comme courbe paramétrée par une exponentielle
merci et concernant la redaction et la methode que j'ai ecrit sont elle juste
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 23 Juin 2015, 08:42
par paquito » 23 Juin 2015, 08:42
Si tu préfères, on peut l'écrire comme ça:
=\frac{1}{2}cos(\frac{\pi}{2}-\theta))
=\frac{1}{2}sin(\frac{\pi}{2}-\theta))
,
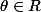
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 23 Juin 2015, 08:48
par adamNIDO » 23 Juin 2015, 08:48
paquito a écrit:Si tu préfères, on peut l'écrire comme ça:
=\frac{1}{2}cos(\frac{\pi}{2}-\theta))
=\frac{1}{2}sin(\frac{\pi}{2}-\theta))
,
merci mais s'il vous pait avant d'ecrire votre methode est ce que la mienne est juste et bien rediger
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 23 Juin 2015, 10:06
par paquito » 23 Juin 2015, 10:06
Non, ça e va pas du tout, tu mets des équivalences en dépit du bon sens, du genre`

????
En plus

, comme

décrit

,

décrit

aussi; tu peut même te limiter à

Tu peux aussi visualiser tout ça sur géogébra; tu définis A(0; 1), B(1; 1) et Z comme image de B dans la rotation de centre A et d'angle a un réel défini sur sur un curseur avec

; puis C(0.5; 0) et Z' l'image de C dans la rotation de centre O et d'angle 1;57-a.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités


est une surjection de
sur le disque unité