Idéal premier !

par **barbu23** » 20 Nov 2009, 19:02

Bonsoir à tous : :happy3:
Soit

et

deux corps tels que

et

.
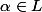
Soit l'homomorphisme d'anneaux définit par :

tel que :

si

et

.
Soit

le noyau de

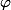
, c'est un idéal de

.
Supposons que

est algebrique sur

, dans ce cas :

par passage au quotient ! On deduit que

est premier !
Je comprends pas pourquoi en conséquence que

est premier !
Merci de votre aide ! :happy3:

par **barbu23** » 20 Nov 2009, 19:09

On precise que c'est parceque :

est intègre ! mais pourquoi,

est intègre ?
Merci de votre aide ! :happy3:

par **barbu23** » 20 Nov 2009, 19:15

Parceque

est un corps est donc

est anneau intègre, par conséquent

est intègre ! c'est ça ?
Mais moi je ne suis pas sûr de ce théorème ! Ce qui est sûr est que

( anneau des polynomes en

) est intègre quant

est un corps !
Merci de me clarifier ce point ! :happy3:

par **Ben314** » 20 Nov 2009, 19:23

Sauf erreur de ma part, dans le contexte dans lequel tu en parle, K[\alpha] est vu comme UNE PARTIE du corps L !!!
Et il est bien clair que tout corps (et, en conséquence tout anneau contenu dans un corps) est intègre.

par **barbu23** » 20 Nov 2009, 19:27

Ah d'accord, c'est vrai ! merci ! :happy3:

par **barbu23** » 20 Nov 2009, 19:34

Salut :
J'ai une autre questipon à vous poser :
Pourquoi si

est un corps alors

est algebrique !
MErci d'avance ! :happy3:

par **barbu23** » 20 Nov 2009, 19:40

est solution de quelle polynome dans

:hein:

par **Ben314** » 20 Nov 2009, 20:58

Si K[alpha] est un corps alors 1/alpha est dedans donc il existe un polynôme P tel que 1/alpha=P(alpha) cela implique que alpha est une racine du polynôme XP(X)-1.

P.S. le polynôme n'est pas dans K[alpha] mais dans K[X] !!

Idéal premier !

Idéal premier !

Qui est en ligne