J'avais une petite question, mais je trouve pas l'idée pour résoudre.
Soit un entier naturel n. Considérons
Montrer que
J'ai commencé par regarder ce que c'était
(Je ne sais pas si c'est licite de noter
Merci
Ncdk a écrit:J'ai quelques soucis avec les définitions.
I est un idéal premier si I est strict et siou
.
Mais je n'arrive pas à l'appliquer à l'exercice. Il faudrait prendre pour moi deux polynômes quelconques déjà et voir queest pas dans
, alors ça implique que
est pas dans
et pareil pour
?
Pournon maximal, je me suis dis que
est un idéal, donc il existe pas d'unique idéal de
contenant strictement
et
, car
,
, ...,
sont des idéaux de
, alors directement on voit qu'il y en a pas qu'un seul et unique idéal de
qui contient lui-même et qui est contenu dans l'anneau
L.A. a écrit:Tu t'éparpilles un peu trop à mon avis. Le but de l'exercice (encore faut-il le savoir, j'en conviens) est de te faire remarquer le lien (équivalence) entre "I_n idéal premier" et "n nombre premier". Je pense que quoique que tu fasses, il faudra que tu utilises le fait que 4 n'est pas premier pour arriver à la solution.
Pour la maximalité, tu peux voir que si n divise m (strictement) alors I_n contient I_m (strictement), d'où le résultat puisque 2 divise 4.
Rmq : si un idéal n'est pas premier, il ne peut pas être maximal...
Ncdk a écrit:Pour rebondir sur l'exercice, j'ai deux questions qui suivent et dont je suis pas trop sur de ma réponse.
2) Soitl'injection canonique de
dans
qui à tout entier
associe le polynôme constant égal à
et soit
la projection canonique. On pose
. Montrer que
est un morphisme surjectif de
sur
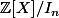
Réponse : Je sais pas si déjà on a le droit, étant donné que c'est pas dit, de dire que p et i sont des morphismes, car on est en présence d'anneaux, donc je vois pas pourquoi c'est pas dit, peut-être que dans la définition même de la projection canonique, c'est que c'est un morphisme. Je voulais vous demandez
Sinon aprèsmais comme
alors
.
étant un morphisme surjectif, alors
est un morphisme surjectif.
3) Déterminer le noyau deet en déduire que

Réponse : Ker=
)=0)

J'arrive pas à trouver, mais je pense que c'est, mais pas tellement d'idée, si je peux avoir une indication, je pense que le fait que
est un idéal peut me servir
Donc il reste à prendre deux applications, la première qui est la projection canonique dedans
, elle est surjective, et une autre qui va de
dans
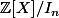
tel que la composée des deux applications ci-dessus donne
Du coup on a déjà un renseignement certain sur l'application que je vais noté, on sait qu'elle est surjective.
Injectivité : J'ai pas encore trouvé, mais si je peux avoir une petite indication merci
MouLou a écrit:Salut. Je ne pesne pas que par définition ce sont des morphismes, mais la vérification est tellement évidente quand on l'écrit qu'on s'embete plus à le dire (et je pense que c 'est tout le temps vrai).
Ensuite, le fait que p est surjectif n'implique pas du tout que p o i est surjective!!
écrit la définition de la surjectivité, et rends toi compte que dire que h est surjective est revient à dire que tout élément d'une classe deadmet un représentant constant (et lequel?)
Pour le 3e c'est aussi assez flou, écrit proprement la définition du noyau (deja le noyau doit etre un idéal de Z puisque ton morphisme part de Z! et des idéaux de Z y'en a pas 50.
D'une manière générale, les notions de quotient ont l'air assez fraiches pour toi et tu sembles encore maladroit dans la manipulation. Je te suggere vraiment d'écrire très scrupuleusement toutes les définitions des objets que tu manipules (par exemple le quotient, la surjectivité etc) , cela viendra alors au fur et à mesure.
Ncdk a écrit:Salut,
Mais pourtant pour tout n, i(n) c'est n.
Donc pour tout n, poi c'est p. Donc p(n)=h(n), comme p est surjective, h l'est aussi vu qu'ils sont égaux. Par égalité si h est surjective, vu que c'est la composé de deux applications dont une est surjective, alors l'autre l'est non ?
J'ai fait une coquille, je vais corriger ici pour le Ker, tu me diras si c'est mieux
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :