Groupes quotients

[sniperamine]

oit t une permutation de S4 avec t=( 1 2 3 4) et p=(12)
( 2 3 4 1 )
soit D le sous groupe {id,t,t²,t^3,p,tp,t²p,t^3p)

expliciter l'ensemble quotient D/


voilà j'ai déjà posté ce petit problème mais personne m'avait répondu merci d'avance pour vos réponses

[sniperamine]

toujours personne :cry:

[yos]

{Id,t²} est une classe, {t,t^3} une autre, {p,t²p} une troisième, {tp,t^3p} la dernière.
Ces quatres classes forment l'ensemble D/ qui n'est pas un groupe pour la loi induite.

[sniperamine]

{Id,t²} est une classe, {t,t^3} une autre, {p,t²p} une troisième, {tp,t^3p} la dernière.
Ces quatres classes forment l'ensemble D/ qui n'est pas un groupe pour la loi induite.

oui merci YOS c'est bien ça mais comment tu fais pour les trouver ?

[yos]

La classe (à gauche) de x modulo un sous-groupe H est l'ensemble xH, c'est à dire l'ensemble des xh où h décrit H.
Prenons ici la classe de l'élément t : elle contient tId et tt², c'est-à-dire t et t^3.

[sniperamine]

La classe (à gauche) de x modulo un sous-groupe H est l'ensemble xH, c'est à dire l'ensemble des xh où h décrit H.
Prenons ici la classe de l'élément t : elle contient tId et tt², c'est-à-dire t et t^3.

ah ok merci t'as oublié pt non ?

[yos]

t'as oublié pt non ?

Non. La classe de pt est {(pt)Id,(pt)t²}, c'est-à-dire {}
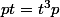
A noter que et .

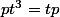
[yos]

p=(12) ( 2 3 4 1 )

C'est plutôt p=(13)

[sniperamine]

ok merci yos non p=(12)

[yos]

tp serait d'ordre 3 : impossible.