J'étudie les groupes fondamentaux et, pendant mon étude, je suis tombé sur une preuve que je n'arrive pas à comprendre. Un théorème stipule que, pour
Problème de conceptualisation de groupes quotients
8 messages
- Page 1 sur 1
Problème de conceptualisation de groupes quotients
Bonjour,
J'étudie les groupes fondamentaux et, pendant mon étude, je suis tombé sur une preuve que je n'arrive pas à comprendre. Un théorème stipule que, pour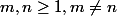 , on a que
, on a que \rangle} \not \simeq \frac{\mathbb{Z}^m}{\langle(2,2,\dots,2)\rangle}) . La première étape de la preuve consiste à montrer que, lorsque
. La première étape de la preuve consiste à montrer que, lorsque 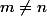 , on a que
, on a que 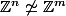 . Or, dans la preuve, on utilise le résultat suivant :
. Or, dans la preuve, on utilise le résultat suivant : ^n \simeq \frac{\mathbb{Z}^n}{2\mathbb{Z}^n}) . J'ignore si c'est un problème de visualisation de ma part ou un problème de notation, mais je ne comprends pas comment ces groupes peuvent être isomorphes, le groupe de gauche étant fini et le groupe de droite étant infini. Il me semble que le groupe de gauche est
. J'ignore si c'est un problème de visualisation de ma part ou un problème de notation, mais je ne comprends pas comment ces groupes peuvent être isomorphes, le groupe de gauche étant fini et le groupe de droite étant infini. Il me semble que le groupe de gauche est
^n = (\frac{\mathbb{Z}}{2\mathbb{Z}})^n) qui contient
qui contient  éléments, mais le groupe de droite est
éléments, mais le groupe de droite est \rangle}) , qui contient une infinité d'élément (en particulier,
, qui contient une infinité d'élément (en particulier, } \neq \overline{(0,0,0, \dots,0,j)} \forall i \neq j) ). Est-ce que je visualise mal le groupe de droite?
). Est-ce que je visualise mal le groupe de droite?
J'étudie les groupes fondamentaux et, pendant mon étude, je suis tombé sur une preuve que je n'arrive pas à comprendre. Un théorème stipule que, pour
Oui, vu que, par définition du quotient, on aDavid R. a écrit:Est-ce que je visualise mal le groupe de droite ?
Et la preuve de l'isomorphisme est immédiate : cela vient du fait que l'application "canonique"
En fait, en regardant de plus prés, là où tu te gourre, c'est que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Oui, vu que, par définition du quotient, on aDavid R. a écrit:Est-ce que je visualise mal le groupe de droite ?
Et la preuve de l'isomorphisme est immédiate : cela vient du fait que l'application "canonique"
En fait, en regardant de plus prés, là où tu te gourre, c'est que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Oui, vu que, par définition du quotient, on ace qui équivaut à i-j pair et pas à i=j.
Et la preuve de l'isomorphisme est immédiate : cela vient du fait que l'application "canonique"est surjective et a pour noyau
.
En fait, en regardant de plus prés, là où tu te gourre, c'est que. Par exemple
mais
Voilà voilà! Merci beaucoup.
Doraki a écrit:C'est bizarre parceque moi j'utilise que Z^n/2Z^n n'est pas isomorphe à Z^m/2Z^m pour montrer que Z^n n'est pas isomorphe à Z^m alors que toi j'ai l'impression que tu fais l'inverse.
Non, je n'utilise que ça, et ensuite je compte le nombre d'éléments dans chacun des groupes quotients. Mon problème était avec la conceptualisation de ces groupes quotients : je ne les croyais pas finis et ne comprenais pas en quoi l'argument était suffisant.
J'ai une seconde question, reliée à ça. Je suis maintenant convaincu que
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
