Gradient d'une fonction

[alexyuc]

Bonjour,

Après un bon moment sans faire de mathématiques pures, me voici devant un exercice de calcul différentiel en optimisation. Il s'agit du gradient (matrice des dérivées partielles d'une fonction f).

1. Quelle est le gradient de , fonction de dans telle que


où est une matrice carrée de taille x

2. Que devient cette expression quand est symétrique ?

Après quelques essais particuliers avec des matrices de taille 2x2 ou 3x3 je n'arrive pas à conclure à une formule générale. Pourriez-vous me donner quelques indices ?

Merci de votre aide

[Pythales]

est une forme bilinéaire de la forme
soit
Si est symétrique,

[Maxmau]

bonjour
Montre que f(x+h) - f(x) = x*(A+A*)h + ||h|| E où E tend vers zéro avec h ( x*= transposé de x , A* = transposée de A)
La différentielle de f en x est donc la forme linéaire h ------>x*(A+A*)h
d'où le gradient de f en x

[alexyuc]

Merci Pythales et Maxmau pour vos réponses.

Je suis tombé sur le résultat à ma question qui dit que le gradient est en reprenant la notation de Maxmau.
Quand A est symétrique on a donc A = A* donc le gradient devient

Cependant, malgré ce que vous avez dit précédemment je ne vois pas comment parvenir à ce résultat. Que devient le h en fait ?

Merci encore

[Maxmau]

La différentielle de f en x est donc la forme linéaire h ------>x*(A+A*)h
le gradient est le vecteur qui multiplié scalairement par h est égal à x*(A+A*)h (pour tout h)
le gradient de f en x est donc le vecteur (A+A*)x

[zygomatique]

salut



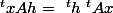
or avec de matrice carrée ... quand on travaille sur R ....

...