Normaliser le gradient d'une fonction

[Brisingle]

Bonjour,
Je me suis tenté à un défi informatique mais sur le chemin de sa résolution, un problème mathématique a surgit ! Je me suis efforcé à essayer de le résoudre... sans succès... Je me tourne alors vers vous en espérant que vous pourrez m'aider.
Le problème est le suivant :
J'ai une fonction f : R→RxR, et pour tout x dans R, f(x) = (x, cos(x))
On a alors pour tout x dans R, grad(f(x)) = (1, -sin(x))
Et ||grad(f(x))|| = sqrt(1 + sin²(x))
Le problème est la... il me faut ||grad(f(x))|| = 1 pour tout x dans R
Alors, comment normaliser le gradient de f.
Vous allez me dire de diviser par f par cette norme mais ce n'est pas si simple car je ne dois pas changer f(R)...

On récapitule :
On a f(x) = (x, cos(x)) pour tout x dans R
Je dois obtenir ||grad(f(x))|| = 1, pour tout x dans R tout en conservant f(R)

Pour résoudre ce problème, je me suis dis que je devais composer f par une fonction g bijective de R dans R pour obtenir h de sorte que h = f o g , que ||grad(h)|| = 1 et que h(R) = f(R). Je n'ai pas trouvé la fonction h qui conviendrait et je n'ai malheureusement pas d'autre idée...

Voilà, Merci de votre attention, en espérant que vous trouverez une solution à ce problème.

[GaBuZoMeu]

Pourquoi appelles-tu gradient ce qui est simplement la dérivée ? C'est un contresens.

Tu as donc . Tu veux reparamétrer ta courbe par la longueur de l'arc, de façon à ce que la vitesse devienne égale à 1. Tu poses et tu veux que soit de norme 1. Vu que (dérivation de fonction composée), tu te retrouves donc à résoudre l'équadiff .

[Brisingle]

Pourquoi appelles-tu gradient ce qui est simplement la dérivée ? C'est un contresens.

Effectivement, je me suis un peut perdu entre les fonctions de qui vont de R → R² et celles qui vont de R² → R.
Mais est ce que ici le gradient et la dérivée ne sont pas la même chose ?

Merci beaucoup pour ta réponse, je n'avais pas du tout pensé a dériver la composé (alors que c'était presque la question ^^'). En plus, informatiquement, cela se fait très bien et tout fonctionne.

Merci et bonne journée

[GaBuZoMeu]

Non, un gradient et une dérivée, ce n'est pas la même chose.

Tu as résolu l'équa diff ? Comment ?

[Brisingle]

Non, un gradient et une dérivée, ce n'est pas la même chose.

Mais dans ce cas, vu que f ne dépend que d'une variable, son gradient c'est sa dérivée non ?

Je ne l'ai pas résolue analytiquement mais numériquement, c'est pour un problème informatique

[tournesol]

Il convient de préciser le vocabulaire .
Il est indépendant du nombre de variables et même de la notion de variable .
F est une application de l'evn E dans l'evn F .
F est differentiable en x si il existe une application lineaire Lx continue telle que au voisinage de x on a :
F(x+h)=F(x) +Lx(h)+o(||h||)
Lx est appelée differentielle de F en x . On la note dFx .
Dans le cas où F est differentiable sur un ouvert O , la dérivee de F est la fonction definie sur O et à valeurs dans (E,F) telle que F'(x)=DFx .
Lorsque E et F sont de dimension finie et rapportés a des bases , DFx possede une matrice dans ces bases notee JFx et nommée jacobienne de F en x . Dans le cas où F est de dimension 1 , cette jacobienne JFx est appelée gradient de F en x . Dans le cas où E et F sont de dimension 1 , ce gradient est aussi appelé nombre dérivé de F en x .
Quid de la fonction dérivée ?
Elle n'a pas changée sauf qu'en dimension finie , on peut définir sur notre ouvert O l'application qui à x fait correspondre JFx . Elle depend des bases .
En dimention 1 elle est appelée aussi fonction dérivée par abus de langage et par necessité pedagogique dans l'enseignement secondaire .
Il ne faut pas faire cet abus de langage inutile pour les fonctions gradient et Jacobienne , mais on le trouve parfois dans l'enseignement superieur .

[GaBuZoMeu]

Pas trop d'accord avec tournesol (au delà de la maladresse de notation qui consiste à appeler F à la fois l'application et l'espace d'arrivée).
Le gradient a un sens pour une fonction définie sur un espace euclidien (ou sur une variété munie d'une métrique riemannienne). C'est un champ de vecteurs sur cet espace ou cette variété. La différentielle d'une fonction est le produit scalaire avec son gradient.
Le gradient a pour composantes les dérivées partielles de la fonction si on travaille dans une base orthonormée ; autrement, ce n'est pas le cas !

Brisingle, serait-ce trop te demander que d'indiquer le problème que tu te posais ?

[tournesol]

Maladresse rime avec paresse. Je n'ai pas voulu utiliser Latex qui m'obligait à écrire 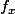, alors j'ai écrit Fx . Bien fait pour moi .
Pour le reste tu n'est pas trop d'accord . Sur quels points ?

[GaBuZoMeu]

Sur ton identification du gradient avec la matrice jacobienne. Il me semble avoir expliqué plus haut ce qu'est le gradient pour moi (et pas que pour moi). Ça me paraît assez différent de la matrice jacobienne.

[tournesol]

Tu parles de gradient comme un champs de vecteurs , je parle de matrice Jacobienne de f en x et de gradient de f en x , ie des valeurs de ce champs en x . Je ne vois pas de désaccord .

[GaBuZoMeu]

Elle depend des bases .

Le gradient ne dépend pas des bases.

[tournesol]

OK merci . Je vais approfondir tout cela .