Vu ce que tu écrit, je me demande s'il n'y a pas un truc qui t'a échappé :
La définition théorique du gradient, c'est pour une fonction

où

est un espace Euclidien (voire un Hilbert), c'est à dire muni d'un produit scalaire.
Et dans ce cas, le gradient est défini par de
.h=\,<\nabla_f (x)\, |\, h>)
(produit scalaire).
Dans le cas où

, le produit scalaire de deux vecteurs colonne

et

c'est

(qui est une matrice

qu'on identifie à un réel).
Mais dans le cas où

est un espace de matrice, le produit scalaire, ça va être comme d'habitude la somme des produit terme à terme :
\ ;\ B\!=\!(b_{i,j})\ \Rightarrow\ <\!A\,|\,B\!>\,=\sum_{i,j}a_{i,j}b_{i,j})
(=un réel) et n'est surement pas égal à

(vu que c'est une matrice) mais qui vaut en fait
)
(la trace).
Sinon, concernant les gradients, ce que j'ai écrit, c'est que :
1)
\big)-\ln\big(\det(A)\big)=\ln\big(\det(I\!+\!A^{-1}H)\big)\simeq\ln\big(1\!+\!\mbox{tr}(A^{-1}H)\big)\simeq\mbox{tr}(A^{-1}H))
Ce qui signifierais que le gradient de
\big))
c'est
^{T})
qui, vu l'indication (1), m'a laissé perplexe jusqu'à ce que je réalise que ta grosse fonction

a comme espace de départ l'ensemble des matrices symétriques (définies positives).
2)
V)\big)-\ln\big(\det(I\!+\!AV)\big)\simeq\mbox{tr}\big((I\!+\!AV)^{-1}HV\big)=\mbox{tr}\big(V(I\!+\!AV)^{-1}H\big))
(car
\!=\!\mbox{tr}(BA))
). Donc le gradient de
\big))
ça serait
^{-1}\big)^{T})
qu'on peut un peu simplifier vu que

est supposée symétrique.
Sauf que, arrivé à ce point, j'ai laissé tombé vu qu'il y a forcément quelque chose qui m'a échappé : l'indication (1) ne me semble correcte que lorsque

est symétrique alors que la matrice

avec laquelle on doit utiliser l'indication n'a pas de raison de l'être.
Et d'ailleurs, je ne comprend pas non plus pourquoi les déterminant des matrices

devraient être >0 (pour prendre le logarithme) alors qu'on a aucune hypothèses sur les matrices
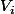
...
