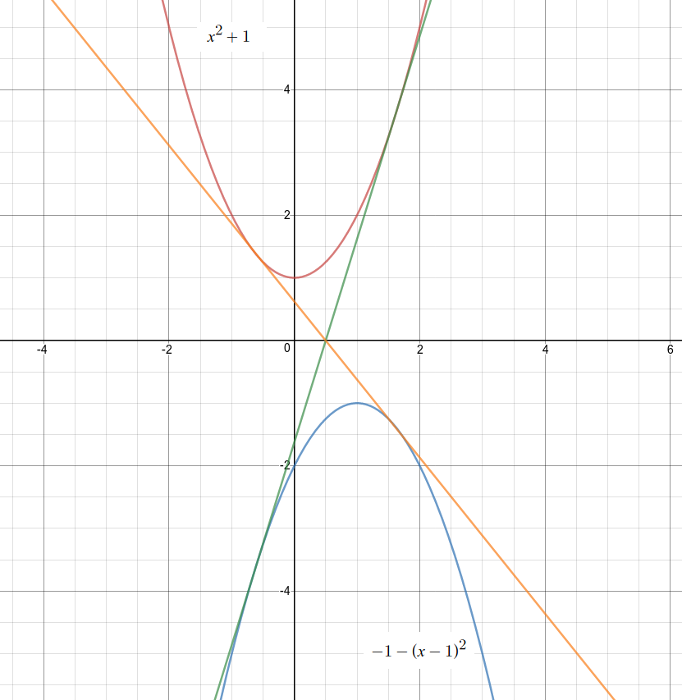Bonjour j' ai une question pour entrer en Master et je ne sais pas du tout comment faire, tout aide serait la bievenue, voici la question :
Trouver un nombre A qui soit le coefficients angulaire de la droite simultanement tangeante aux deux paraboles d'equation :
y= x^2 + 1 et y= -1 - (x-1)^2
Arrondir A 3 chiffres après la virgule
Voila Merci d'avance !
Géometrie BAC +3
8 messages
- Page 1 sur 1
Re: Géometrie BAC +3
tu écris l'équation d'un tangente au point d'abscisse a à la première parabole.
le système d'équation d'intersection entre cette droite et la seconde parabole a une solution double (deltas nuls) quand on est sur des deux tangentes communes.
tu dois trouver 2 tangentes possibles
le système d'équation d'intersection entre cette droite et la seconde parabole a une solution double (deltas nuls) quand on est sur des deux tangentes communes.
tu dois trouver 2 tangentes possibles
Re: Géometrie BAC +3
pascal16 a écrit:tu écris l'équation d'un tangente au point d'abscisse a à la première parabole.
le système d'équation d'intersection entre cette droite et la seconde parabole a une solution double (deltas nuls) quand on est sur des deux tangentes communes.
tu dois trouver 2 tangentes possibles
J'ai du mal a poser le systeme :
-2x+2= x^2+1 ?
J'obtient x = -1 +ou- racine(2)
Mais comment obtenir le coefficient angulaire
Re: Géometrie BAC +3
c'est quoi le x que tu as trouvé ?
[edit] : ça à l'air d'être une abscisse, mais de quoi ?
[edit] : ça à l'air d'être une abscisse, mais de quoi ?
Modifié en dernier par pascal16 le 02 Mai 2018, 13:24, modifié 1 fois.
Re: Géometrie BAC +3
J'obtient x = -1 +ou- racine(2)
en posant la derivé de la deuxieme parabole egale a l'quation de la premiere parabole
merci d'avance
en posant la derivé de la deuxieme parabole egale a l'quation de la premiere parabole
merci d'avance
Re: Géometrie BAC +3
MHann a écrit:J'obtient x = -1 +ou- racine(2)
en posant la derivé de la deuxieme parabole egale a l'quation de la premiere parabole
merci d'avance
salut
il faut revoir le raisonnement
Si une droite non verticale coupe une parabole en un seul point, elle lui est tangente.
Tu cherches des droites d'équation y=ax+b.
Il est nécessaire que les deux équations ci-dessous aient chacune une unique solution.
ax+b=x²+1
et
ax+b=-1-(x-1)²
Les discriminants doivent être nuls.
On peut faire autrement.
Re: Géometrie BAC +3
Salut,
Si on veut résumer, pour traduire qu'une droite est tangente à la parabole d'équation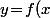\!=\!x^2\!+\!1) tu peut
tu peut
(1) Soit dire que son équation est de la forme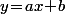 et que l'équation du second degré
et que l'équation du second degré ) admet une unique solution (i.e. que le discriminant est nul).
admet une unique solution (i.e. que le discriminant est nul).
(2) Soit dire que son équation est de la forme(x\!-\!x_1)\!+\!f(x_1)) pour un certain
pour un certain 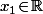
Idem pour traduire qu'elle est tangente à la parabole d'équation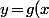\!=\!-1\!-\!(x\!-\!1)^2) où tu peut
où tu peut
(1') Soit dire que son équation est de la forme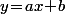 et que l'équation du second degré
et que l'équation du second degré 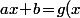) admet une unique solution (i.e. que le discriminant est nul).
admet une unique solution (i.e. que le discriminant est nul).
(2') Soit dire que son équation est de la forme(x\!-\!x_2)\!+\!g(x_2)) pour un certain
pour un certain 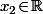 .
.
L'indication donné par pascal16, c'est de prendre (2) puis (1').
L'indication donné par chan79, c'est de prendre (1) puis (1').
Donc vu que j'ai plus le choix, on va dire que "mon" indication, c'est (2) puis (2').
(en fait en terme de difficulté et longueur de calculs, c'est tout kif-kif...)
Si on veut résumer, pour traduire qu'une droite est tangente à la parabole d'équation
(1) Soit dire que son équation est de la forme
(2) Soit dire que son équation est de la forme
Idem pour traduire qu'elle est tangente à la parabole d'équation
(1') Soit dire que son équation est de la forme
(2') Soit dire que son équation est de la forme
L'indication donné par pascal16, c'est de prendre (2) puis (1').
L'indication donné par chan79, c'est de prendre (1) puis (1').
Donc vu que j'ai plus le choix, on va dire que "mon" indication, c'est (2) puis (2').

(en fait en terme de difficulté et longueur de calculs, c'est tout kif-kif...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :