Géodésique de la sphère avec Euler-Lagrange
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
par Wenneguen » 27 Sep 2014, 17:39
Bonjour,
je dois trouver la courbe de longueur minimale qui rejoint deux points d'une sphère.
Après calculs (que je peux détailler si vous voulez), j'aboutis à :
=\int_{\varphi_0}^\varphi \dfrac{K}{\sqrt{1-K^2 \sin^2 t}} dt + \theta(\varphi_0))
où
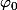
est quelconque et
est une constante obtenue par l'équation d'Euler-Lagrange.
Le souci est que je ne vois pas comment calculer cette intégrale. Pensez-vous que j'ai fait une erreur quelque part, ou bien y a-t-il une astuce ?
Merci :we:
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
par Cliffe » 27 Sep 2014, 18:00
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
par Wenneguen » 27 Sep 2014, 18:02
Oui Maple m'a sorti cette fonction, mais je suis censé trouvé l'équation d'un cercle dont le centre est le centre de la sphère, donc je ne crois pas que répondre avec cette fonction soit acceptable :hum:
-
mathelot
par mathelot » 27 Sep 2014, 18:03
Wenneguen a écrit:
Après calculs (que je peux détailler si vous voulez):
oui, volontiers, ça m'intéresse.
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
par Cliffe » 27 Sep 2014, 18:04
Si maple n'y arrive pas c'est pas la peine de venir posté sur le fofo ^^
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
par Wenneguen » 27 Sep 2014, 20:49
mathelot a écrit:oui, volontiers, ça m'intéresse.
En notant
l'abscisse curviligne de la courbe étudiée, je dis qu'on a
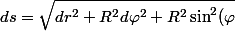 d\theta^2}=\sqrt{R^2 d\varphi^2+R^2 \sin^2 (\varphi) d\theta^2)
puisque
est constant.
La longueur de la courbe vaut alors :
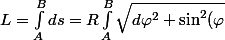d\theta^2} = R\int_A^B \sqrt{1+\sin^2(\varphi) \left(\dfrac{d\theta}{d\varphi}\right)^2}d\varphi)
.
L'équation d'Euler-Lagrange s'écrit :
 - \dfrac{\partial F}{\partial \theta})
avec
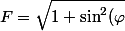 \dot{\theta}^2})
et
.
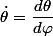
On a
\dot{\theta}^2}})
et
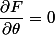
, donc d'après Euler-Lagrange :
=0)
et donc
\dot{\theta}^2}} = K)
où K est une constante.
En mettant au carré puis en isolant
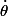
, j'obtiens
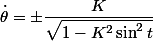
, d'où finalement
=\pm \int_{\varphi_0}^\varphi \dfrac{K}{\sqrt{1-K^2 \sin^2 t}} dt + \theta(\varphi_0))
.
-
mathelot
par mathelot » 27 Sep 2014, 20:59
merci beaucoup.
Après changement de variable
)
)
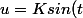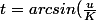on trouve , sauf erreur
Il me semble que c'est du domaine des intégrales elliptiques, étudiées (et répertoriées) par Jacobi.
merci encore, bonne soirée.
-
mathelot
par mathelot » 27 Sep 2014, 21:03
Qu'est ce que ça donne, par curiosité, avec une métrique Riemannienne sur une surface hyperbolique (courbure négative)
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
par Wenneguen » 27 Sep 2014, 23:53
Merci, mais en supposant que je n'ai pas fait d'erreur, comment montrer que ceci correspond à un grand cercle ?
Désolé mais je n'ai aucune idée de ce qu'est une surface Riemannienne :livre:
Je sors tout juste de prépa et il y a une semaine je ne connaissais pas l'équation d'Euler-Lagrange :hein:
-
mathelot
par mathelot » 28 Sep 2014, 07:27
peut être qu'un grand cercle admet une paramétrisation particulière en
;\phi(t)))
à ce moment là, on remplace
et
par
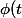
) et
)
pour s'assurer que cette paramétrisation vérifie l'équation intégrale .
(l'adjectif "intégral" est utilisé quand les équations sont écrites à l'aide de quadratures)
-
sinusx
- Membre Naturel
- Messages: 16
- Enregistré le: 26 Sep 2009, 16:08
-
par sinusx » 28 Sep 2014, 09:08
Salut,
Dans
ce document (partie 2.2), une reparamétrisation du Lagrangien permet d'obtenir les équations des grands cercles.
-
Ben314
- Le Ben
- Messages: 21696
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 28 Sep 2014, 15:18
Salut,
Il me semble qu'il y a un bug là :
Wenneguen a écrit: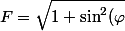\dot{\theta}^2}})
ça ne serait pas plutôt
\dot{\theta}}{ \sqrt{1 + \sin^2(\varphi)\dot{\theta}^2}}\ \)
?
D'où
 \sqrt{\sin^2(\varphi)-K^2}\ \)
Arrivé à ce point, il faut que tu intègre cette équa. diff. pour montrer qu'elle a pour solution un truc du style
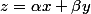
en coordonnées cartésiennes (grand cercle = plan passant par l'origine)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Wenneguen
- Membre Relatif
- Messages: 202
- Enregistré le: 15 Oct 2011, 18:53
-
par Wenneguen » 29 Sep 2014, 11:49
Ben314 a écrit:Salut,
Il me semble qu'il y a un bug là : ça ne serait pas plutôt
?
D'où
Arrivé à ce point, il faut que tu intègre cette équa. diff. pour montrer qu'elle a pour solution un truc du style
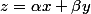
en coordonnées cartésiennes (grand cercle = plan passant par l'origine)
Exact j'ai oublié un
)
en dérivant, mais malheureusement ça ne semple pas simplifier les choses ! :hum:
-
Ben314
- Le Ben
- Messages: 21696
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 29 Sep 2014, 14:32
 \sqrt{\sin^2(\varphi)-K^2}}\ \ \Rightarrow\ \ \theta(\varphi)=\pm\int_{?}^{\varphi}\frac{K}{\sin(t) \sqrt{\sin^2(t)-K^2}}dt\ +Cst)
Tu veut obtenir un truc du style
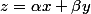
en coordonnées cartésiennes,
c'est à dire
=\alpha\sin(\varphi)\cos(\theta)+ \beta \sin(\varphi)\sin(\theta)\)
en polaire
soit encore
=\gamma\cos(\theta+Cst)\)
(où
)
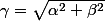
et donc
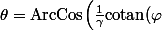\Big)-Cst\)
Ca incite évidement à faire le changement de variable
\)
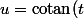dans l'intégrale qui donne
=\frac{1}{1+u^2}\)
et
:
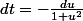
\ <br />=\ \pm\int_{?}^{\text{cotan}(\varphi)}\frac{K}{\sqrt{\frac{1}{1+u^2} } \sqrt{\frac{1}{1+u^2}-K^2}}\times -\frac{du}{1+u^2}\ +Cst\ <br />=\ \mp\int_{?}^{\text{cotan}(\varphi)}\frac{K\, du}{\sqrt{1-K^2(1+u^2)}}\ +Cst)
qui s'intègre gentiment avec de l'ArcCosinus et qui donne bien le résultat escompté.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
