Géodesique comment trouver l équation

[Anonyme]

Bonjour ,

je serai content de pouvoir discuter avec une personne afin de comprendre
comment trouver l equation d une géodésique (courbe d acceleration nulle)

[busard_des_roseaux]

Bj,

Il semble que ce problème mélange du "local" et du "global":

dans l'espace euclidien, une géodésique entre A et B est la ligne droite
(le vol d'oiseau). Qu'est ce que l'on minimise au juste ?

Sur la sphère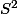 , les géodésiques sont des arcs
de grands cercles.

Les géodésiques doivent tenir compte de la courbure (elle est intrinsèque)
de l'espace mais aussi de sa topographie.

par exemple, dans un labyrinthe, la géodésique vers la sortie
tient compte de l'intégralité de sa configuration.

Ce que l'on résoud,dès la classe de Cinquième, ce sont les géodésiques
du cube:

une fourmi se promène sur les faces d'un cube de A vers B.
on met le cube à plat sur un "patron". On trace la ligne droite de A vers B,
on relève cette ligne droite sur le cube. Sur le patron ,
des points distincts sont identifiés par le recollement des arêtes,
ce qui peut donner plus d'une géodésique.

Dans les mathématiques du supérieur (!), il semble que le cadre d'étude
soient les variétés Riemanniennes ou pseudo-Riemanniennes.
On cherche alors à minimiser une fonctionnelle d'énergie
sur un ensemble de lacets tracés sur la variété.
(variété=surface)