Bonjour,
Avant tout chose, merci de lire cette conversation
En effet l'énoncé est "Soit la suite Xn = somme de k=1 à n de ln k - n ln n + n - 1/2 ln n"
J'ai donc grâce à cette conversation réussit à montrer grâce à abcd22 que xn - xn+1 est équivalent en +oo et que la suite converge. On me demande alors la question suivante :
Dans cette question, on tentera d'établir la formule de Sterling. En vous servant des résultats précédents,
a) Etablir l'existence d'une constante strictement positive C telle que n! soit équivalent en +oo à C (n/e)^n racine (n)
b) Etablir la formule de Stirling, n! équivaut à (n/e)^n racine (2 pi n )
Et la je bloque vraiment :briques: Si vous avez des idées, merci d'avance ! :++:
Formule de Stirling
9 messages
- Page 1 sur 1
Hum dans l'exercice je vois pas trop non c'était les intégrales de Wallis avant, avec l'étude de l'intégrale de 0 à pi/2 de cos x a la puissance n. Etude classique : démontrer que la fonction est décroissante, que In+1 est équivalent à In, trouver Un equivalent à (2n)^p / 2n! si je me souviens bien... bref pas grand chose qui m'aide !
Ah ben voilà, je pensais justement aux intégrales de Wallis pour trouver la valeur de C ! :happy3:
On a dû vous faire calculer explicitement les valeurs des intégrales, en remplaçant les factorielles qui sont dedans par^n) on trouve un équivalent de
on trouve un équivalent de 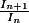 , on en déduit la limite de
, on en déduit la limite de 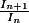 en fonction de C, et on a aussi
en fonction de C, et on a aussi  ...
...
On a dû vous faire calculer explicitement les valeurs des intégrales, en remplaçant les factorielles qui sont dedans par
Ah non point du tout, on nous a pas fait calculer les valeurs des intgrales. On a montré :
- que la suite In est decroissante avec In ) integrale 0 à pi/2 cos x puissance n
- que In=2 = (n+1 / n+2)In
- que I2p = ((2p)! / 2^2p(p!)^2)(pi/2)
- que In est équivalent en +oo à racine de pi / racine de 2(n+1)
Mais en fait faut absolument que je finisse l'exo pour demain, je capte vraiment rien pour savoir comment on fait pour trouver C ! Par contre je voudrais au moins faire la question a mais avec tes calculs deja je vois pas comment on élimine la somme et comment on fait disparaitre les ln car meme en passant à l'exponentielle, je veux bien mais dans ce cas la on a e^Xn or ce que je cherche ùpo c'est Xn !
Si t'as le temps - mais je pense que j'abuse - , tu voudrais pas m'expliciter les calculs ?
En tout cas merci pour tout le reste c'est génial !
- que la suite In est decroissante avec In ) integrale 0 à pi/2 cos x puissance n
- que In=2 = (n+1 / n+2)In
- que I2p = ((2p)! / 2^2p(p!)^2)(pi/2)
- que In est équivalent en +oo à racine de pi / racine de 2(n+1)
Mais en fait faut absolument que je finisse l'exo pour demain, je capte vraiment rien pour savoir comment on fait pour trouver C ! Par contre je voudrais au moins faire la question a mais avec tes calculs deja je vois pas comment on élimine la somme et comment on fait disparaitre les ln car meme en passant à l'exponentielle, je veux bien mais dans ce cas la on a e^Xn or ce que je cherche ùpo c'est Xn !
Si t'as le temps - mais je pense que j'abuse - , tu voudrais pas m'expliciter les calculs ?
En tout cas merci pour tout le reste c'est génial !
Pour le b) avec ce que tu as ça marche aussi : dans l'expression de  tu remplaces les factorielles par
tu remplaces les factorielles par ^n) , il y a plein de simplifications et on trouve
, il y a plein de simplifications et on trouve  , on a aussi
, on a aussi }} \sim \frac{\sqrt\pi}{2\sqrt{p}}) , on en déduit que
, on en déduit que  .
.
Pour le a) :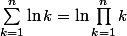} = \ln{(n!)}) ,
,
 ,
,
 ,
,
et .
.
En additionnant tout ça et en utilisant encore la propriété du logarithme on a : .
.
On a montré que la suite convergeait vers une limite
convergeait vers une limite  , donc
, donc  converge vers
converge vers  . Comme
. Comme  , ça signifie que
, ça signifie que  et on multiplie par
et on multiplie par ^n) pour avoir l'équivalent de n!.
pour avoir l'équivalent de n!.
Pour le a) :
et
En additionnant tout ça et en utilisant encore la propriété du logarithme on a :
On a montré que la suite
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
