Formule pour le logarithme népérien d'un nombre ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Yezu
- Membre Relatif
- Messages: 335
- Enregistré le: 14 Fév 2018, 12:29
-
 par Yezu » 03 Sep 2018, 03:37
par Yezu » 03 Sep 2018, 03:37
Bonjour à tous,
Dans un de mes cours de physique, à un moment dans les notes; le prof utilise cette formule :
 = \lim_{n \to \infty} n(\sqrt[n]{x} - 1}))
en écrivant quelques lignes plus tard qu'il utilise ce résultat "facilement démontrable".
Par curiosité, je cherche à le démontrer; mais je n'y arrive pas vraiment.
Est-ce qu'il faut passer par :
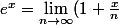^n)
?
Merci d'avance.
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 03 Sep 2018, 07:46
par Kolis » 03 Sep 2018, 07:46
Bonjour !
Tu prends
=\ln(\sqrt[n]x)^n=n\ln(\sqrt[n]x))
et si tu sais que la limite de
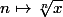
est 1, il y a un équivalent classique pour le logarithme.
Il est clair que tout ça ne vaut que pour

.
-
Yezu
- Membre Relatif
- Messages: 335
- Enregistré le: 14 Fév 2018, 12:29
-
 par Yezu » 03 Sep 2018, 08:39
par Yezu » 03 Sep 2018, 08:39
Merci beaucoup Kolis !
Je pense avoir compris la preuve ^^
Bonne journée
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités