Bonjour à tous,
Je viens de lire dans un bouquin de mathematiques comment a été construite la fonction logarithme népérien :
Voiçi ce qui se dit dans ce livre :
" Nous avons tendance dans cette exercice de détérminer toutes les fonctions

, définies sur l'intervalle
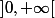
, verifiant les deux propriétés suivantes :
 ~~ $)
.
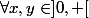
:
 = f(x) + f(y) $)
 ~~ $)
.

est dérivable sur
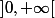
.
Solution :
La fonction nulle sur
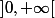
verifient les deux propriétés de l'enoncé.
Supposons qu'il existe une autre fonction

differente de la fonction nulle et qui verifient les deux conditions précédentes.
On a :
 = 1 $)
( On prend dans
 ~~ $)
:

) .
On considère la fonction

définie sur
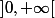
comme suit :
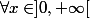
:
 = f(xy) = f(x ) + f(y) $)
.
On a :
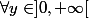
:
 = x f'(xy) = f'(y) $)
Si on prend :
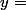
, on obtient :
 = \frac{f'(1)}{x} $)
.
Si on prend :
 = k $)
, alors :
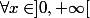
:
 = \frac{k}{x} $)
avec :
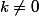
.
On constate de ce qui prècède que

est la fonction primitive de la fonction :
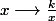
sur
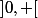
et qui s'annule en

. Cette fonction existe car,
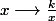
est continue sur
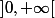
.
Inversement, Soit

la fonction primitive de
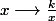
sur
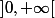
et qui s'annule en

.

est dérivable sur
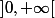
et
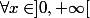
:
 = \frac{k}{x} $)
.
Montrons que :
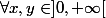
:
 = F(x) + F(y) $)
.
On considère la fonction :

définie sur
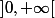
comme suit :
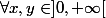
:
 = F(xy) $)
.
On a :
 = x F'(xy) = x. \frac{k}{xy} = \frac{k}{y} $)
.
Alors,

est une primitive de
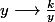
sur
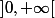
, et donc :
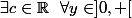
:
 = F(y) + c $)
.
Puisque :
 = 0 $)
, alors :
 = F(x) = c $)
D'où,
 = F(x) + F(y) $)
.
Conclusion :
Les fonctions définies et dérivables sur
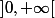
verifiant les deux conditions de l'énoncé est la fonction primitive de la fonction
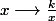
et qui s'annule en

.
Questions :
 ~~ $)
Pourquoi choisit - on de definir

sur
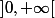
et non sur
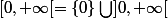
ou bien sur tout

?
 ~~ $)
Peut - t - on suivre la même démarche pour determiner toutes les fonctions

definies sur un intervalle à trouver :

telles que :
 ~~ $)
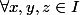
:
 = f(x) + f(y) + f(z) $)
.
 ~~ $)

est dérivable sur

.
?
Merci d'avance de vos reponse.
