Oui tu as raison, c'est moi, ça me gêne un peu parce que je n'avais pas vu la démo de cette formule sous cet angle :
- soit on démontrais cette formule sous forme trigonométrique :
)^n = \cos(n\theta) + i \sin(n\theta ))
puis après on notais
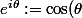 + i\sin(\theta ))
pour écrire
^n = e^{in\theta })
.
- soit on établissait par récurrence que
=n \arg(z))
puis on établissait la formule de De Moivre en comparait modules et argument.
Mais dans les deux cas, normalement on traite d'abord la forme trigonométrique puis exponentielle d'un nombre complexe.
Le truc qui me gêne un peu c'est que
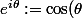 + i\sin(\theta ))
n'est qu'une notation et que certaines propriétés relatives à cette notation coïncident bien avec celle de l'exponentielle réelle. Du coup, c'est dur de savoir si la personne en question (pas forcément mehdi-128) sait bien ce qu'elle fait ou si elle tente d'appliquer des propriétés sur un objet similaire à l'exponentielle réelle. Mais là c'est un autre débat

