Formule à démontrer

[Simpi]

Bonjour, je cherche à démontrer ses deux formule mais je n'y arrive pas, j'ai besoin de votre aide:
Démontrer que
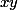
1) si est strictement inferieur à

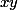
2) si est strictement supérieur à 1 ou .

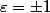
[Black Jack]

Prendre la tangente des 2 membres ...

En se rappelant que tan(x+b) = (tan(a) + tan(b))/(1 - tan(a).tan(b))

Avec les précautions d'usages ... (par exemple en tenant compte que tan() est Pi périodique)

[Robot]

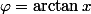
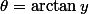
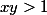
A mon avis, il vaut mieux débuter en posant , et interpréter la condition en condition portant sur les angles et .

[aymanemaysae]

Bonjour,

la méthode de M. Robot est la plus simple et la plus directe, mais j'aimerais proposer une solution pour la première question un peu moins directe, tout en vous incitant de suivre la méthode que vous a proposée M.Robot car c'est la plus pédagogique et vous y apprendrez beaucoup d'astuces sur les .

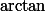
Supposons que : donc on a .

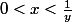
Posons ,

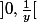
donc f'(x) = 0 , donc comme f est continue sur alors f y est constante .

On a aussi , donc

ce qui implique que .

[aymanemaysae]

reBonjour,

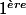
une autre façon de procéder pour la question .

Comme on a : càd

,

donc ,

donc

donc .

[Robot]

Rien ne dit que et sont strictement positifs.

[Simpi]

Bonjour, j'ai suivi la methode proposée par M.Robot, alors si je pose
et je trove la formule démandée
maintenant si
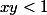
-si et sont strictement positif alors:
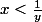
ce qui implique que
or
donc on aura
par consequent
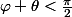
- de meme si et sont strictement négatif on montrera que
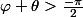
puisque dans ce cas

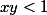
En conclusion on dira que si alors .
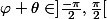
j'espere que c'est ca.

[aymanemaysae]

Bonjour;

M.Robot, vous avez raison, je n'ai étudié qu'un cas parmi les quatre possibles.

Le cas où x et y sont strictement négatifs est similaire au cas où x et y sont strictement positifs, donc il reste les deux cas où x et y sont de signes contraires.

1) Si

donc

2) Si

donc .

Je crois que les quatre cas sont maintenant étudiés .

Un grand Merci à M.Robot, pour son aide et pour sa patience.

[Robot]

Si je pose
et je trove la formule démandée

Que veux-tu dire ????

Moi, je trouve juste
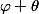
d'un côté, et de l'autre.

Il reste à examiner quand ces deux quantités sont égales.

Il peut être utile de faire un dessin :
D''un côté le plan des avec les zones délimitées par
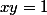
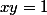
De l'autre le carré des , avec les zones délimitées par ce qui correspond à . (Tu as pratiquement fait le boulot, il faut juste un peu plus de soin).

Aymane, ne te crois pas obligé de faire l'exercice à la place de Simpi.