Bonjour,
||.|| désigne la norme euclidienne de

, S désigne la sphère unité. On note
)
la base canonique de

Pour
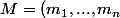 \in M_{n,n} (R))
on définit son permanent de
)^n)
dans

par :
=\sum_{\sigma \in \mathfrak{S}_n}m_{1 \sigma(1)} \times ... \times m_{n \sigma(n)})
Soit V un sous espace vectoriel de

on dira que
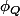
est définie positive (respectivement positive, respectivement définie négative) sur V lorsque :
 >0)
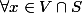
respectivement
 \geq 0)
respectivement
 <0)
On notera
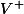
l'ensemble des sous espaces vectoriels sur lesquels
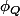
est définie positive, respectivement
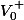
et
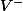
On note
=max_{V \in V^+} (dim V))
et
=max_{V \in V^-} (dim V))
Soient R et Q des matrices réelles inversibles de taille n telles qu'il existe une constante k satisfaisant :
 - B_R (x,y)| \leq k ||x|| \times ||y||)
On a montre qu'il existe
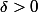
tel que :
=s(\phi_Q))
si
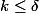
Maintenant soit
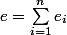
,
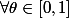
on pose :
=per(\theta m_1 + (1-\theta)e,...,\theta m_{n-2} + (1-\theta)e,x,y))
On montre facilement que :
=1)
et
=n-1)
Soient

et
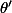
2 éléments distincts de [0,1], on admet que pour tout x,y de

:
 - B_{\theta'} (x,y)| \leq n \times n!|\theta - \theta'| \times ||x||\times||y|| \prod_{j=1}^{n-2} (||m_j||+ \sqrt{n}))
Je bloque sur cette question :
Établir que
=1)
et
=n-1)
On pourra raisonner par l'absurde et considérer :
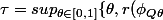=1\})
J'y arrive pas


