Forme modulaire sur un réseau.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 09 Fév 2009, 13:00
Bonjour :happy3:
Je souhaite étudier la fonction définie par :
=\Bigsum_{\omega \in \Omega-\{0\}} \frac{1}{\omega^{2n}})
où
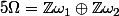
est un réseau de
.
On la voit aussi comme une fonction du demi-plan de Poincaré
:
=\Bigsum_{(p,q)\in (\mathbb{Z}*)^{2}} \frac{1}{(p\omega+q)^{2n}})
en prenant
.
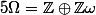
J'ai démontré que la série était absolument convergente avec la majoration :
où C est telle que
et en identifiant
à un réseau
.
Je souhaite démontrer à présent que c'est une
forme modulaire. J'ai quasiment tout fait, il me reste à montrer qu'elle est
holomorphe en 
.
J'ai trouvé en fouillant un peu dans mes bouquins que
=2\zeta(2n))
.
Comment démontrer cette formule?.
Autre question :
Dans la suite j'ai besoin d'un résultat, je dois démontrer que pour une fonction f holomorphe sur le disque unité et tout complexe z d'un disque fermé de rayon
:
}(z)|^{2}\le \lambda_{n}\Bigint_{\mathbb{U}} |f(\zeta)|d\zeta)
avec
une constante dépendant de n.
Je prends
et j'arrive en appliquant Cauchy à :
}(z)|\le \frac{n!}{2\pi(\beta-\alpha)}\Bigiint_{[\alpha,\beta]\times [0,2\pi]} \frac{|f(\rho e^{i\theta})|}{(\rho-R)^{n-1}}d\rho d\theta)
mais je ne vois pas comment arriver à ma constante, c'est surement tout bête ...
Merci (désolé de la longueur du message...) :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 09 Fév 2009, 14:13
Correction, je trouve plutôt :
}\;\;\Bigiint_{[\alpha,\beta]\times [0,2\pi]}\;\;\frac{|f(\rho e^{i\theta})|}{(\rho-R)^{n+1}}\rho d\rho d\theta)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 09 Fév 2009, 16:59
Petit up. :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 09 Fév 2009, 17:08
Arf, c'était effectivement tout con ma deuxième question, c'est du
Cauchy-Schwartz :
}(z)|^{2}\le \(\frac{n!}{2\pi}\)^{2} \[ \Bigiint_{[\alpha,\beta]\times [0,2\pi]} |f(\rho e^{i\theta})|^{2}\rho d\rho d\theta\]\times \[ \Bigiint_{[\alpha,\beta]\times [0,2\pi]} \frac{\rho}{(\rho-R)^{2n+2}}d\rho d\theta\])
Bon il me manque plus que ma première question !
-
R.C.
- Membre Relatif
- Messages: 134
- Enregistré le: 22 Nov 2008, 10:37
-
par R.C. » 09 Fév 2009, 17:43
Bonjour
Nightmare a écrit:Arf, c'était effectivement tout con ma deuxième question, c'est du
Cauchy-Schwartz :
}(z)|^{2}\le \(\frac{n!}{2\pi}\)^{2} \[ \Bigiint_{[\alpha,\beta]\times [0,2\pi]} |f(\rho e^{i\theta})|\rho d\rho d\theta\]\times \[ \Bigiint_{[\alpha,\beta]\times [0,2\pi]} \frac{\rho}{(\rho-R)^{n+1}}d\rho d\theta\])
Bon il me manque plus que ma première question !
Il est bizarre ton cauchy schwarz : il manque pas des carrés sous les intégrales?
Pour la première question, j'ai l'impression que si tu découpe ta somme en mettant les termes avec p =0 d´un côté et le reste de l'autre tu dois pouvoir montrer la formule. Pour ce qui est de l'holomorphie, remplace
par
dans phi et montre que c'est holomorphe en 0.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 09 Fév 2009, 17:49
Oups bien entendu, je corrige !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 09 Fév 2009, 17:51
Pour la première question, oui le seul problème est de démontrer la formule, une fois chose faite elle nous donne directement que la fonction est holomorphe à l'infinie.
Oui j'ai essayé de découper la somme, ça ne marche pas...
-
R.C.
- Membre Relatif
- Messages: 134
- Enregistré le: 22 Nov 2008, 10:37
-
par R.C. » 09 Fév 2009, 18:08
=\Bigsum_{q\in (\mathbb{Z}*}) \frac{1}{q^{2n}} + \Bigsum_{(p,q)\in (\mathbb{Z}*\times\mathbb{Z}}) \frac{1}{(p\omega+q)^{2n}} = 2\zeta(2n)+ \Bigsum_{(p,q)\in (\mathbb{Z}*\times\mathbb{Z}}) \frac{1}{(p\omega+q)^{2n}})
, et le deuxiéme terme tend vers 0 (en majorant brutalement avec des modules et en séparant partie réelle et imaginaire)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 09 Fév 2009, 18:21
Il y a un soucis, pourquoi prends-tu p=0 alors qu'on l'exclu dès le départ?
=\Bigsum_{p\in \mathbb{Z}*\\q\in \mathbb{Z}*} \frac{1}{(p\omega+q)^{2n}})
donc je ne vois pas ce qui autorise ton découpage!
-
R.C.
- Membre Relatif
- Messages: 134
- Enregistré le: 22 Nov 2008, 10:37
-
par R.C. » 09 Fév 2009, 18:40
Tu es sûr que tu dois enlever les couples (0,q) et (p,0) (j'avais pas fais attention) ? Parce que à ce moment là ça fait 0 en l'infini.
Il me semblait que d'habitude pour les formes modulaires on sommait sur tous les éléments du réseau, sauf 0.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 09 Fév 2009, 18:50
Non tu as raison, q est non nul mais p peut l'etre, j'ai mal lu mon document...
Donc on a en effet :
=2\zeta(2n)+2\Bigsum_{p=1}^{+ \infty}\Bigsum_{q\in \mathbb{Z}} \frac{1}{(p\omega+q)^{2n}})
et le terme de droite converge tranquillement vers 0 (on peut meme le calculer je pense !).
Effectivement, avec un bon énoncé, ça devient plus simple !
Merci de ton aide ! :happy3:
(PS : désolé pour les accents circonflexes manquant, problème informatique, ils ne se tapent plus...
)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 09 Fév 2009, 23:30
Juste pour avoir confirmation, pour montrer que c'est une forme modulaire, j'ai aussi démontré que, pour une matrice
\in SL_{2}(\mathbb{Z}))
,
=\phi_{2n}\(\mathbb{Z}\oplus\frac{a\omega+b}{c\omega+d} \mathbb{Z}\)=...=(c\omega+d)^{2n}\phi_{2n}(\omega))
Le raisonnement est bon?
-
R.C.
- Membre Relatif
- Messages: 134
- Enregistré le: 22 Nov 2008, 10:37
-
par R.C. » 10 Fév 2009, 09:38
J'ai pas fais le calcul, mais c'est ça qu'il faut faire.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 10 Fév 2009, 19:46
D'accord je te remercie :happy3:
L'article est très intéressant, il démontre avec l'aide des formes modulaires l'indépendance algébriques de certains nombres transcendants.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 11 Fév 2009, 01:13
J'ai été un peu vite en besogne dans ma preuve de convergence, ma majoration est complètement fausse.
On a plutot :
Pour un
fixé.
^{2n}}{\epsilon} \Bigsum_{\omega\in\Omega-\{0\}} \Bigiint_{D(\omega,r)} \frac{dxdy}{(x^2+y^2)^n})
.
Le membre de droite est fini (calcul simple).
:happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
