Bonsoir a tous.
Je dois montrer que si on prend u une une forme lineaire de E un K espace normé (K=R ou C),u est continue ssi Ker(u) est un fermé de E.
la premiere implication est immédiate,mais je ne vois pas comment faire la réciproque.
Merci de votre aide.
Forme lineaire continue
7 messages
- Page 1 sur 1
par Nightmare » 28 Mai 2008, 20:47
Salut !
Soit y tel que = 1)
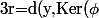On a) > 0)
On considère)
On a}\in Ker(\phi))
puisque }\)=\phi(y)-\frac{1}{\phi(x)}\phi(x)=0)
Ainsi}\)=||y-\(y-\frac{x}{\phi(x)}\)||=\frac{||x||}{\phi(x)})
On en déduit|\le \frac{||x||}{r})
vraie aussi pour x nul.
Comme alors |\le \frac{1}{2}\le 1)
ce qui montre la continuité.
Soit y tel que
On a
On considère
On a
Ainsi
On en déduit
Comme
par maxboubou » 28 Mai 2008, 21:11
merci de ta réponse,mais on utilise ou le fait que Ker(u) est fermé ?
par Nightmare » 28 Mai 2008, 21:13
C'est ce qui nous permet d'écrire que d(y,Ker(phi)) n'est pas nulle (tout en sachant que y n'est pas dans Ker(phi))
par chococoo » 28 Mai 2008, 21:33
euh,juste pour vérifier,elle est continue,car bornée sur une boule fermée ?
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :