Bonjour,
Je travaille actuellement un cours sur les fonctions continues et il y a une partie que je n'arrive pas à comprendre.
Ca dit :
La fonction f : R dans R définie par f(x) = x² est continue sur R. En effet, si a appartient à R, on a :
| f(x) - f(a) | = | x - a | | x + a | <= | x - a |² + 2|a||x - a|
D'où sort le | x - a |² + 2|a||x - a| ? Pourquoi ont - ils mit ça et pas (| x - a | | x + a |)² ou autre chose par exemple ? Pourquoi cette valeur là ?
Ensuite, ça dit :
Soit Epsilon > 0. On a :
| x - a | < inf ( 1, epsilon / ( 2|a| + 1) IMPLIQUE | f(x) - f(a) | < Epsilon
Je n'ai absolument rien compris. D'abord pourquoi | x - a | < inf ( 1, epsilon / ( 2|a| + 1) et ensuite en quoi l'un applique l'autre.
Merci d'avance pour votre aide.
Fonctions continues
8 messages
- Page 1 sur 1
OrsayMPI a écrit:Bonjour,
Je travaille actuellement un cours sur les fonctions continues et il y a une partie que je n'arrive pas à comprendre.
Ca dit :
La fonction f : R dans R définie par f(x) = x² est continue sur R. En effet, si a appartient à R, on a :
| f(x) - f(a) | = | x - a | | x + a | 0. On a :
| x - a | < inf ( 1, epsilon / ( 2|a| + 1) IMPLIQUE | f(x) - f(a) | < Epsilon
Je n'ai absolument rien compris. D'abord pourquoi | x - a | < inf ( 1, epsilon / ( 2|a| + 1) et ensuite en quoi l'un applique l'autre.
Merci d'avance pour votre aide.
salut
vois avec x+a=x-a+2a
Pour montrer la continuité de f(x) en a on veut pouvoir montrer qu'on peut rendre la distance entre f(x) et f(a) aussi petite qu'on veut en choisissant x suffisement proche de a, on est donc amené à travailler la quantité |f(x)-f(a)| à l'aide de la quantité |x-a| ( |a - b| représentant la distance entre a et b ) d'où l'idée de faire apparaître cette dernière quantité et regarder comment la choisir pour rendre la première inférieure à n'importe quelle valeur fixée à l'avance ( epsilon ).
OrsayMPI a écrit:Merci, grâce à vous deux j'ai réussis à comprendre une grosse partie. Cependant je bloque toujours sur le
| x - a | < inf ( 1, epsilon / ( 2|a| + 1) IMPLIQUE | f(x) - f(a) | < Epsilon
Comment arrive - t - on à déterminer que | x - a | < inf ( 1, epsilon / ( 2|a| + 1) ?
On ne le détermine pas, on suppose qu'on l'a.
Bonjour.
Dans ce genre de calcul,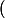 montrer que
montrer que =\mathcal{l})
) , on démarre de
, on démarre de -\mathcal{l}|) et on essaie par majoration successives à avoir
et on essaie par majoration successives à avoir -\mathcal{l}| \le M |x-a|) . On peut être amené a faire des majorations de
. On peut être amené a faire des majorations de 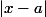 du type
du type 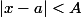 afin de majorer certaines expressions dans les majorations successives de
afin de majorer certaines expressions dans les majorations successives de -\mathcal{l}|) . En prenant
. En prenant 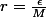 , on aura:
, on aura:
-\mathcal{l}|< M|x-a|< M \frac{\epsilon}{M}= \epsilon) .
.
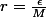 n'est valable que l'on tient compte des majorations faites sur
n'est valable que l'on tient compte des majorations faites sur 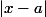 .
.
Si on avait émis l'hypothèse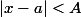 , il faudra changer
, il faudra changer  et prendre
et prendre )
Reprenons l'exemple
 - f(a) | = | x - a | | x + a | \le | x - a |^2 + 2|a||x - a|)
Si l'on suppose que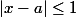 , alors
, alors 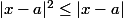 et
et
 - f(a) | = | x - a | | x + a | \le | x - a |^2 + 2|a||x - a| \le | x - a | + 2|a||x - a|=| x - a |(1 + 2|a|))
Pour avoir - f(a) | < \epsilon) , il suffit que
, il suffit que < \epsilon) et pour cela prendre
et pour cela prendre )
Remarques:
On aurait pu supposer que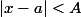 et dans ce cas
et dans ce cas 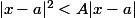 et
et
 - f(a) | = | x - a | | x + a | \le | x - a |^2 + 2|a||x - a| \le A| x - a | + 2|a||x - a|=| x - a |(A + 2|a|)) .
.
On prendra dans ce cas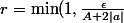)
Dans ce genre de calcul,
Si on avait émis l'hypothèse
Reprenons l'exemple
Si l'on suppose que
Pour avoir
Remarques:
On aurait pu supposer que
On prendra dans ce cas
deltab a écrit:Bonjour.
Dans ce genre de calcul,montrer que
=\mathcal{l})
, on démarre de
et on essaie par majoration successives à avoir
. On peut être amené a faire des majorations de
du type
afin de majorer certaines expressions dans les majorations successives de
. En prenant
, on aura:
.
n'est valable que l'on tient compte des majorations faites sur
.
Si on avait émis l'hypothèse, il faudra changer
et prendre
Reprenons l'exemple
Si l'on suppose que, alors
et
Pour avoir, il suffit que
et pour cela prendre
Remarques:
On aurait pu supposer queet dans ce cas
et
.
On prendra dans ce cas
Bonjour,
C'est très compliqué!
Je ne peux pas répondre.
cadeau de no;)l
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
