Fonction: Y(x,n)= 1/(x-1)^n ?

[ALBIN92]

Bjr, mon niveau est mat elem d'il y a 50 ans !
soit:
f(x)=1/(x-1)
je note que:
f(6) n=1 à … f(7) n=1 à … f(8)

0,166666667 1 0,142857143 1 0,125
0,027777778 2 0,020408163 2 0,015625
0,00462963 3 0,002915452 3 0,001953125
0,000771605 4 0,000416493 4 0,000244141
0,000128601 5 5,9499E-05 5 3,05176E-05
2,14335E-05 6 8,49986E-06 6 3,8147E-06
3,57225E-06 7 1,21427E-06 7 4,76837E-07
5,95374E-07 8 1,73467E-07 8 5,96046E-08
9,9229E-08 9 2,47809E-08 9 7,45058E-09
1,65382E-08 10 3,54013E-09 10 9,31323E-10
2,75636E-09 11 5,05733E-10 11 1,16415E-10
4,59394E-10 12 7,22476E-11 12 1,45519E-11
7,65656E-11 13 1,03211E-11 13 1,81899E-12
1,27609E-11 14 1,47444E-12 14 2,27374E-13
2,12682E-12 15 2,10634E-13 15 2,84217E-14
3,5447E-13 16 3,00906E-14 16 3,55271E-15
5,90784E-14 17 4,29866E-15 17 4,44089E-16
9,8464E-15 18 6,14095E-16 18 5,55112E-17
1,64107E-15 19 8,77278E-17 19 6,93889E-18
2,73511E-16 20 1,25325E-17 20 8,67362E-19
4,55852E-17 21 1,79036E-18 21 1,0842E-19
7,59753E-18 22 2,55766E-19 22 1,35525E-20
0,2 0,166666667 0,142857143

f(6)=1/5 f(7)=1/6 f(8)=1/7

Questions:
a) quelle est cette fonction ?
est-ce: la fonction: Y(x,n)= 1/(x-1)^n ?
b) comment représenter cette fonction en 3 dimensions ?

Merci pour votre aide

[zygomatique]

salut

et tu crois qu'on va comprendre ce charabia ....

[mathelot]

c 'est la fonction

On la représente dans le plan en dimension 2

[ALBIN92]

c 'est la fonction

On la représente dans le plan en dimension 2

Oui, mais alors vous ne prenez pas en compte n. Vous avez réduit ma question.
Je ne pose pas la question pour une fonction dans un espace à 2 dimensions, mais pour un espace à 3 dimensions.
C'est donc un volume et c'est la surface supérieure de ce volume que je voudrais visualiser pour voir les singularités de cette surface.

[ALBIN92]

salut

et tu crois qu'on va comprendre ce charabia ....

Puisqu'il me faut être plus explicite, je redonne le détail du calcul sous excel.
La disposition avait été désorganisée par le copier/coller:
f(x)=1/(x-1)

f(6) n=1 à … f(7) n=1 à … f(8) n=1 à …

0,166666667 1 0,142857143 1 0,125 1
0,027777778 2 0,020408163 2 0,015625 2
0,00462963 3 0,002915452 3 0,001953125 3
0,000771605 4 0,000416493 4 0,000244141 4
0,000128601 5 5,9499E-05 5 3,05176E-05 5
2,14335E-05 6 8,49986E-06 6 3,8147E-06 6
3,57225E-06 7 1,21427E-06 7 4,76837E-07 7
5,95374E-07 8 1,73467E-07 8 5,96046E-08 8
9,9229E-08 9 2,47809E-08 9 7,45058E-09 9
1,65382E-08 10 3,54013E-09 10 9,31323E-10 10
2,75636E-09 11 5,05733E-10 11 1,16415E-10 11
4,59394E-10 12 7,22476E-11 12 1,45519E-11 12
7,65656E-11 13 1,03211E-11 13 1,81899E-12 13
1,27609E-11 14 1,47444E-12 14 2,27374E-13 14
2,12682E-12 15 2,10634E-13 15 2,84217E-14 15
3,5447E-13 16 3,00906E-14 16 3,55271E-15 16
5,90784E-14 17 4,29866E-15 17 4,44089E-16 17
9,8464E-15 18 6,14095E-16 18 5,55112E-17 18
1,64107E-15 19 8,77278E-17 19 6,93889E-18 19
2,73511E-16 20 1,25325E-17 20 8,67362E-19 20
4,55852E-17 21 1,79036E-18 21 1,0842E-19 21
7,59753E-18 22 2,55766E-19 22 1,35525E-20 22
____________ __________ ____________
total =0,2 = 0,166666667 =0,142857143
soit
f(6)=1/5 f(7)=1/6 f(8)=1/7

[SLA]

Puisqu'il me faut être plus explicite, je redonne le détail du calcul sous excel.
La disposition avait été désorganisée par le copier/coller:
f(x)=1/(x-1)

f(6) n=1 à … f(7) n=1 à … f(8) n=1 à …

0,166666667 1 0,142857143 1 0,125 1
[...]
7,59753E-18 22 2,55766E-19 22 1,35525E-20 22
____________ __________ ____________
total =0,2 = 0,166666667 =0,142857143
soit
f(6)=1/5 f(7)=1/6 f(8)=1/7

Quand bien même tes maths remontent à 50 ans, les notations que nous utilisons tous ont plus d'un siècle. Dans ces notations "f(6) n=1 à ..." ne signifie rien. f(6) c'est f(6), il n'y a pas de "n".
D'ailleurs f(6)=1/5 comment obtiens tu le 0.166666...? (qui ressemble plus à 1/6)
Je suppose que ta question est: "j'ai une fonction Y(x,n) dont voici quelques valeurs (pour x=6,7,8 et =1,...,22). Peut-on trouver Y?"
Le fait de travailler à précision finie (comprendre sous excel) empêche de dire qu'il n'y aura qu'une fonction solution.

Ceci dit jai quand même l'impression que ton tableau est celui de .
Cordialement

[ALBIN92]

Quand bien même tes maths remontent à 50 ans, les notations que nous utilisons tous ont plus d'un siècle. Dans ces notations "f(6) n=1 à ..." ne signifie rien. f(6) c'est f(6), il n'y a pas de "n".
D'ailleurs f(6)=1/5 comment obtiens tu le 0.166666...? (qui ressemble plus à 1/6)
Je suppose que ta question est: "j'ai une fonction Y(x,n) dont voici quelques valeurs (pour x=6,7,8 et =1,...,22). Peut-on trouver Y?"
Le fait de travailler à précision finie (comprendre sous excel) empêche de dire qu'il n'y aura qu'une fonction solution.

Ceci dit jai quand même l'impression que ton tableau est celui de .
Cordialement

Bonjour,
Je vois que vous examinez ma demande selon une géométrie en 2 dimensions.
Or je raisonne en 3 dimensions.
C'est à dire que je cherche à représenter une surface (donc intégrale dont la fonction dérivée est la fonction 1/ (1 -x), surface elle même définissant un volume inférieur puisque y, x, et n soit 3 axes. Pourquoi volume inférieur ? Parce que les résultats partiels montrent une décroissance de la sommation....
Ce qui me manque est la base math exprimant ma pensée. Autrement dit, les symboles du langage des maths.
Vous ne dites pas la vérité sur cette question de langage: la formulation symbolique a évolué depuis 50 ans !!!! Quel âge avez-vous ? Si vous n'avez pas plus de 65 ans, vous n'êtes pas qualifié pour en parler !!!!
Je vois simplement que vous n'avez pas compris ma pensée.
Normal, comprendre la pensée d'autrui est chose peu aisée quand le langage ne suit pas.
D'où l'importance de la codification du langage et de l'intérêt des dictionnaires quand les mots sont là !
Dernier point, ce n'est pas parce qu'une expression est incompréhensive pour vous, qu'elle est dénuée de sens......
Sauf pour les jeunots que la vie n'a pas encore rendu sages. Ne pas s'étonner ensuite que certaines expressions soient perçues comme ayant un sens bien des années après.
Merci pour votre participation, bien que je reste dans mon ignorance.....

[Robot]

Comprendre la pensée d'autrui n'est pas chose aisée quand elle est exprimée de manière aussi obscure. Ton histoire de surface et d'intégrale est totalement incompréhensible. Comprends-tu toi-même ce que tu écris ?
Le tableau que tu recopies est sans aucun doute le tableau de avec entier 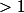et entier 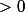, comme l'a déjà dit SLA
Déja, la somme des pour allant de à l'infini est égale à . Rien de surprenant à la somme de tes colonnes, donc !.

[SLA]

Bonjour,
Je vois que vous examinez ma demande selon une géométrie en 2 dimensions.
Or je raisonne en 3 dimensions.
C'est à dire que je cherche à représenter une surface (donc intégrale dont la fonction dérivée est la fonction 1/ (1 -x), surface elle même définissant un volume inférieur puisque y, x, et n soit 3 axes. Pourquoi volume inférieur ? Parce que les résultats partiels montrent une décroissance de la sommation....
Ce qui me manque est la base math exprimant ma pensée. Autrement dit, les symboles du langage des maths.
Vous ne dites pas la vérité sur cette question de langage: la formulation symbolique a évolué depuis 50 ans !!!! Quel âge avez-vous ? Si vous n'avez pas plus de 65 ans, vous n'êtes pas qualifié pour en parler !!!!
Je vois simplement que vous n'avez pas compris ma pensée.
Normal, comprendre la pensée d'autrui est chose peu aisée quand le langage ne suit pas.
D'où l'importance de la codification du langage et de l'intérêt des dictionnaires quand les mots sont là !
Dernier point, ce n'est pas parce qu'une expression est incompréhensive pour vous, qu'elle est dénuée de sens......
Sauf pour les jeunots que la vie n'a pas encore rendu sages. Ne pas s'étonner ensuite que certaines expressions soient perçues comme ayant un sens bien des années après.
Merci pour votre participation, bien que je reste dans mon ignorance.....

Salut,
Non, je n'ai pas de capital vieillesse assez conséquent selon tes critères. Si cette discussion doit être un affrontement "Vieux Vs Jeunes", alors ça ne m'interesse pas. Mais j'insiste: la notation qui exprime une fonction (même de plusieurs variables) est la même depuis belle lurette.
Note quand même que j'ai fais l'effort d'essayer de comprendre ce que tu cherchais, et que malgré cet effort tu n'as pas répondu à ma question: Comment as-tu obtenu ton tableau?

Par ailleurs, une surface c'est bien un objet de dimension 2, quand bien même il "vit" dans un espace de dimension 4 ou plus. Donc la regarder dans un espace de dimension 3 me semble un peu superflu.

Un oncle à moi, qui n'est pourtant pas matheux m'a expliqué un jour qu'on communiquait pour être compris. Si on n'est pas clair, c'est qu'il faut changer la formulation.

Donc étant donné que ta fonction f ne dépend que d'une variable à savoir x, que signifie "f(6) de n=1 à ...".

Bref je n'ai pas compris la question.

cordialement