Fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
par zork » 04 Jan 2012, 20:31
en faites j'aimerai bien faire d'autres exos du même style: définition sur la continuité, prolongement par continuité...
ainsi qu'en analyse sur les définitions: critère de cauchy...
parce que j'ai remarqué que j'avais vraiment du mal :triste: . Quand c'est des exercices simples comme quel est la nature d'une série ou bien si on me donne une fonction à plusieurs variables et on demande sa continuité je saurai le faire car j'ai fais cela en TD. Mais là c'est la galère avec ces exos
sinon pour revenir au sujet du fil:
dans la définition de la continuité on dit que c'est pour tout
. donc en particulier si
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 04 Jan 2012, 20:33
On veut montrer la continuité, on ne l'a pas. Donc il faut montrer que c'est vrai quel que soit epsilon.
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
par zork » 04 Jan 2012, 20:41
j'utilise l'inégalité triangulaire:
-cos(x)|<=|cos(a)-cos(y)|+|cos(y)-cos(x)|)
la fonction cosinus est continue sur R donc
-cos(x)|<=\epsilon)
en particulier au point a
donc
-cos(x)|<2\epsilon)
-
mathelot
par mathelot » 05 Jan 2012, 08:43
tu peux utiliser un DL à l'ordre 1 ,avec reste intégral, entre x et y, pour la fonction
d'une variable réelle sinus().
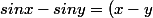cosy +\int_{x}^{y} (t-x) \sin \, t dt)
pour un point
)
de la bissectrice avec
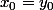
 = cosy - cos y_0 +\frac{\int_{x}^{y} (t-x) \sin \, t dt}{x-y})
-G(x_0,y_0) | \leq |y-y_0| +\frac{1}{2} |y-x|)
-G(x_0,y_0) | \leq |y-y_0| +\frac{1}{2} (|y-y_0|+|x-x_0|))
-G(x_0,y_0) | \leq \frac{3}{2} ||(x,y)-(x_0,y_0)||_1)
G est localement lipschitzienne (en plus de la continuité)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
