Fonction

[zork]

en utilisant le TAF: sin(x)-sin(y)=(x-y)cos(x)



en prenant

on a la continuité

[Nightmare]

Je ne comprends pas de quelle définition de la continuité tu pars et ton application du TAF est incorrecte!

[zork]

je pars de cette définition: http://upload.wikimedia.org/wikipedia/fr/math/0/5/c/05c05b716a931984c96349861f083989.png

[Nightmare]

Ca, c'est la définition dans R, ici on est plus dans R mais dans R². Il faut que tu fasses un effort pour réfléchir aux objets que tu manipules, ce n'est pas difficile, mais si tu ne réfléchis pas tu ne t'en sortiras pas.

[zork]

après j'ai adapté la définition:

[Nightmare]

Ok, cela dit, il peut être beaucoup plus pratique de faire un changement de variable pour se ramener à une limite en (0,0).

Concernant ton application du TAF, essaye de la revoir car ça ne va pas du tout.

[zork]

pourquoi mon application du taf est incorrecte?

je pend la fonction sinus qui est dérivable

[Nightmare]

Relis le TAF et relis ce que tu as écrit, il y a une grosse erreur au niveau du cos(x).

[zork]

l'erreur vient du x car on est dans l'intervalle ]x,y[

[Nightmare]

Que dit le TAF exactement?

[zork]

si f est dérivable sur R alors quels que soient x,y dans R, il existe a dans ]x,y[ tel que
f(x)-f(y)=f'(a)(x-y)

[Nightmare]

D'accord, ce n'est donc pas exactement ce que tu avais écrit.

Peux-tu corriger?

[zork]

du coup c'est |cos(a)-cos(x)|

[Nightmare]

Non, d'où ça vient ça?

Je sens que tu as un problème mais je n'arrive pas à déterminer lequel. Est-ce un problème de lecture? De symbolique?

Tu me cites un théorème dans lequel il suffit de remplacer par les données de l'exercice, et tu n'y arrives pas alors qu'il n'y a rien de plus facile.

Attention ne te méprend pas, je ne te juge pas, j'essaye au contraire de cerner tes difficultés pour mieux y répondre, mais j'avoue avoir beaucoup de mal à te cerner!

[zork]

je reprend le taf
j'ai écris: f(x)-f(y)=f'(a)(x-y)
c'est là même chose que

dans ce que j'ai fais au départ j'ai pris:

du coup j'utilise le taf sur
ce qui me donne |cos(a)-cos(x)|

[barbu23]

Salut : :happy3:
Pour la fermeture de il suffit de remarquer que :
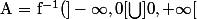avec un homeomorphisme ( i.e. : ).
et donc :

[Nightmare]

dans ce que j'ai fais au départ j'ai pris:

du coup j'utilise le taf sur
ce qui me donne |cos(a)-cos(x)|

Ok, dans ce cas c'est bon, mais il ne faut pas oublier de préciser qui est a, car c'est important pour la suite.

Comment conclure?

[zork]

là j'aurai majoré par 2 car et je prend
donc c'est continue

[zork]

j'aurais une question qui n'a rien à voir avec ce qui précède:

est que les exos que j'ai postés jusqu'à présent comme celui-là (à part les séries) c'est de la topologie
si non dans quel catégorie sont-ils?

[Nightmare]

Désolé j'avais oublié ce topic.

La majoration par 2 est bonne mais en quoi te permettrait-elle d'en déduire la continuité, je ne comprends pas...

Sinon, la topologie est l'étude des formes géométriques et de leur déformation. Ici, il n'est pas question de cela. Cet exercice est un exercice d'analyse.