Fonction somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Laure22
- Messages: 4
- Enregistré le: 18 Sep 2016, 09:23
-
 par Laure22 » 18 Sep 2016, 15:56
par Laure22 » 18 Sep 2016, 15:56
Bonjour,
Pour n € N*, on considère la fonction fn définie sur R+ par:
fn(x)=x+2²+3x^3+...+nx^n=∑ kx^k (k=1 →n)
1/ Un scilab => Fait
2/ Montrer que l'équation fn(x)=1 admet une unique solution que l'on notera Un => J'ai fait fn(x)-1=0. Je pensais utiliser le théorème de la bijection continue mais j'arrive pas à trouver les conditions. Le signe somme me bloque

3/ Je serais débloquée avec la question précédente.
4/ a) =>Fait
b) Montrer fn(x)=x*[1-(n+1)x^n+nx^(n+1)/(1-x)² => Je bloque aussi, je vois que ∑xk (k=1→n)=[1-x^(n+1)]/1-x] mais à partir là je vois pas.
c) Idem que la trois
d) Idem que la trois
Merci d'avance!
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 18 Sep 2016, 16:40
par jlb » 18 Sep 2016, 16:40
Salut, déjà, as-tu constaté que la fonction fn est croissante sur R+
Ensuite calcule fn(0) et fn(1) et tu pourras conclure avec le th de la bijection.
( si tu peines avec fn et le signe somme, commence avec f1 en écrivant directement l'expression , puis f2 et soyons fou f3!!!)
(pour fn(1) tu vas trouver une somme bien connue normalement)
On te donne la formule; fais une récurrence!!

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 18 Sep 2016, 16:52
par zygomatique » 18 Sep 2016, 16:52
salut
pour tout k > 0 la fonction

est strictement croissante sur
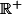
donc sur [0, 1]
une somme de fonctions strictement croissantes est strictement croissante ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 20 Sep 2016, 13:47
par arnaud32 » 20 Sep 2016, 13:47
pour
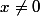
= \sum_{k=0}^{n}kx^k= \frac{1}{x}\sum_{k=0}^{n}kx^{k+1} \\= \frac{1}{x}\sum_{k=0}^{n}[x^{k}]'= \frac{1}{x}[\sum_{k=0}^{n}x^{k}]' \\ =\frac{1}{x}[\frac{1-x^{n+1}}{1-x}]')
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités

