Fonction riemann integrable

[yodelf]

soit f une fonction Riemann intégrable tel que int_0 à +oo f(x) dx converge Comment montrer que si limite de f existe alors elle est égale a zéro? montrer que cette limite vaut zéro quand f est uniformément continue.................. J'ai essayer avec cauchy par l'absurde mais j'y arrive pas.merci

[Nicolas_75]

Bonjour,

Comment montrer que si limite de f existe alors elle est égale a zéro?

Supposons que la limite existe et soit strictement positive égale à L.
Alors, au-dessus d'un certain réel A, f(x) >= L/2
Intègre pour finir le raisonnement par l'absurde...

Nicolas

[laki]

bonsoir

juste une remarque, je chipote mais bon ...
pourquoi supposer la limite de f strictement positive, d'autant plus qu'on a pas d'hypothèses sur le signe de f ? je pense que la supposer non nul suffit.

a la prochaine

[muse]

Pcq pourquoi faire compliqué quand on peut faire simple ? Si ça limite est négative alors tu prends -f ce qui ne change rien.
A un moment faudra bien savoir si la limite est positive ou non et faire un choix de toute maniere.

[laki]

bonsoir yodelf

je ne suis pas sûr de comprendre l'intêret de l'hypothèse d'uniforme contnuité ?

le résultat reste vrai sans elle puis la démo proposée ne l'utilise pas ...

[laki]

bonsoir muse

je te donne une démo, dis moi ce que tu en penses, pour ma part, je la trouve plus naturelle :

f --> L (supposée non nulle) en +oo
alors pour e>0, il existe A>0 tq pour tt x >=a, |f(x)-L|<=e en particulier pour e=(1/2)*|L|>0, on a pour tt x>=a, 0.5*|L|<=|f(x)|, là on intègre sur [A, H]et par comparaison on deduit que f n'est pas intégrable sur [A;+oo[ contradiction et resultat !

pas besoin d'hyp sur la limite ! mais bon comme j'ai dit, je chipote ...

a plus

ps : excuse mais je ne maitrise pas bien le latex ...

[SimonB]

bonsoir yodelf

je ne suis pas sûr de comprendre l'intêret de l'hypothèse d'uniforme contnuité ?

le résultat reste vrai sans elle puis la démo proposée ne l'utilise pas ...

Je suppose qu'il s'agit de montrer que dans le cas où la fonction est uniformément continue, cette limite EXISTE (et vaut automatiquement 0).

J'avoue ne pas l'avoir prouvé, mais c'est un résultat qui me semble vrai.

[SimonB]

pas besoin d'hyp sur la limite ! mais bon comme j'ai dit, je chipote ...

Comme l'a dit muse, on peut remplacer f par -f, ce qui montre que le problème est symétrique du point de vue du signe de la limite.
Comme on préfère généralement les nombres positifs, on traite plus volontiers le cas L>0... sans perte de généralité.

[Doraki]

Soit f uniformément continue et intégrable sur un voisinage de +l'infini.

Soit e > 0.
f est uniformément continue donc soit a > 0 tel que |x-y| < a => |f(x)-f(y)| < e/2.
f est intégrable donc soit x tel que pour tout y,z> x-a, | l'intégrale de f sur [y,z] |< a*e.
Supposons qu'il existe y > x tel que |f(y)| > e
Alors pour tout z de [y-a ; y+a], |f(z)| > e/2
Donc | l'intégrale de f sur [y-a ; y+a] | > a*e, ce qui contredit le choix de x.
Donc |f(y)| < e pour tout y > x.

Donc f tend vers 0.

[Lemniscate]

L'hyposthèse d'uniforme continuité est nécessaire si f n'a pas de limite en +oo. Mais la, comme f a une limite, je ne vois pas où l'uniforme continuité sert. En tout cas je ne trouve pas d'exemples de fonctions continues (pas uniformément) sur [0,+oo[, possédant une limite réelle l, dont l'intégrale de Riemann converge, où l différent de 0.

En revanche, il existe des exemples de fonctions continues sur [0,+oo[, dont l'intégrale de Riemann converge, qui n'ont pas de limite.

Par exemple la fonction f définie sur [0,+oo[ par
, si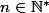
et f affine ailleurs.
[en fait on pourrait mettre f(n)=n, et adapter la définition, ainsi limite de en +oo = +oo et pourtant l'intégrale de Riemann existe !]

on a
(somme des aires de triangle).

Il est clair que f est continue, que son intégrale de Riemann existe (somme de Riemann cv car 2>1) et que pourtant f n'a pas de limite en +oo.

On peut même définir une fonction dérivable en "lissant" f précédente.

Pour les puristes : .

Voila ! Prévenez moi si vous avez des exemples de fonctions continues (pas uniformément) sur [0,+oo[, possédant une limite réelle l, dont l'intégrale de Riemann converge, où l différent de 0.

[SimonB]

L'hyposthèse d'uniforme continuité est nécessaire si f n'a pas de limite en +oo. Mais la, comme f a une limite, je ne vois pas où l'uniforme continuité sert. En tout cas je ne trouve pas d'exemples de fonctions continues (pas uniformément) sur [0,+oo[, possédant une limite réelle l, dont l'intégrale de Riemann converge, où l différent de 0.

Et heureusement : il n'en existe pas. Ce que l'énoncé veut dire, c'est que si tu prends une fonction uniformément continue et intégrable, alors elle possède une limite en l'infini et que cette limite est 0.

En revanche, il existe des exemples de fonctions continues sur [0,+oo[, dont l'intégrale de Riemann converge, qui n'ont pas de limite.

Oui...

[en fait on pourrait mettre f(n)=n, et adapter la définition, ainsi limite de en +oo = +oo et pourtant l'intégrale de Riemann existe !]

Non... Si f a une limite elle est forcément nulle (pas seulement si la limite est réelle). En revanche tu peux effectivement trouver une fonction non bornée qui soit intégrable.

[Lemniscate]

Non... Si f a une limite elle est forcément nulle (pas seulement si la limite est réelle). En revanche tu peux effectivement trouver une fonction non bornée qui soit intégrable.

Oui je me suis un peu emporté ! C'est déjà bien non bornée !

Ce que l'énoncé veut dire, c'est que si tu prends une fonction uniformément continue et intégrable, alors elle possède une limite en l'infini et que cette limite est 0.

Ok mais la façon dont yodelf a posé l'énoncé n'était pas très claire je trouve, ca m'a un peu embrouillé !

Merci, Bye