Fonction paire et impaire
17 messages
- Page 1 sur 1
fonction paire et impaire
Mon prof d'analyse nous a demander de démontrer que toute fonction de
R---->R se décompose de manière unique en somme d'une fonction paire et d'une fonction impaire.
Déja on sait qu'une fonction paire c'est :
pour tout x appartient à Df, f(-x) = f(x)
une fonction impaire c'est :
pour tout x appartient à Df, f(-x) = -f(x)
Donc on veut montrer que :
h:R--->R
avec h(x) = (f(-x) ou f(x)) + (f(-x) ou -f(x))
Est-ce que je commence bien déja ??
R---->R se décompose de manière unique en somme d'une fonction paire et d'une fonction impaire.
Déja on sait qu'une fonction paire c'est :
pour tout x appartient à Df, f(-x) = f(x)
une fonction impaire c'est :
pour tout x appartient à Df, f(-x) = -f(x)
Donc on veut montrer que :
h:R--->R
avec h(x) = (f(-x) ou f(x)) + (f(-x) ou -f(x))
Est-ce que je commence bien déja ??
Bonjour,
commencez par regarder les conditions nécessaires :
soit , telles que f paire, g impaire et h=f+g.
, telles que f paire, g impaire et h=f+g.
Alors f=h-g. Et que vaut h(-x)? Déduisez-en la valeur de f.
Même raisonnement pour trouver la valeur de g.
Il ne reste plus qu'à montrer que les f et g trouvées vérifient bien les hypothèses.
Bon courage et n'hésitez pas à demander de l'aide si ça coince!
commencez par regarder les conditions nécessaires :
soit
Alors f=h-g. Et que vaut h(-x)? Déduisez-en la valeur de f.
Même raisonnement pour trouver la valeur de g.
Il ne reste plus qu'à montrer que les f et g trouvées vérifient bien les hypothèses.
Bon courage et n'hésitez pas à demander de l'aide si ça coince!
Salut, en fait on peut très bien trouver h et g en raisonnant par conditions nécessaires,
c'est-à-dire que tu poses f = g+h et que tu supposes g paire, h impaire,
alors tu exprimes f(x) et f(-x), ça te donne un système, ensuite tu additionnes ou soustraits les 2 lignes ainsi obtenues, ce qui en utilisant la parité de g et h te permet d'exprimer g et h en fonction de f, et de trouver le f et le h de l'énoncé.
Cette méthode a pour mérite de prouver directement l'unicité en même temps que l'existence, car puisqu'on peut remonter les égalités les fonctions g et h trouvées vérifient évidemment les conditions souhaites, ce qui est d'ailleurs immédiat d'après leurs expressions.
c'est-à-dire que tu poses f = g+h et que tu supposes g paire, h impaire,
alors tu exprimes f(x) et f(-x), ça te donne un système, ensuite tu additionnes ou soustraits les 2 lignes ainsi obtenues, ce qui en utilisant la parité de g et h te permet d'exprimer g et h en fonction de f, et de trouver le f et le h de l'énoncé.
Cette méthode a pour mérite de prouver directement l'unicité en même temps que l'existence, car puisqu'on peut remonter les égalités les fonctions g et h trouvées vérifient évidemment les conditions souhaites, ce qui est d'ailleurs immédiat d'après leurs expressions.
J'ai beau écrire des lignes et des lignes de calcul ben j'arrive a rien :
On pose f = g +h
avec g paire et h impaire.
Ona donc : g(x) = g(-x) et h(x) = -h(x).
On aurait alors :
f(x) = g(x) + h(x) ou f(x) = g(-x) -h(x).
Donc la je crois que j'ai correctement exprimer f(x) mais pour f(-x) j'y arrive pas...
On pose f = g +h
avec g paire et h impaire.
Ona donc : g(x) = g(-x) et h(x) = -h(x).
On aurait alors :
f(x) = g(x) + h(x) ou f(x) = g(-x) -h(x).
Donc la je crois que j'ai correctement exprimer f(x) mais pour f(-x) j'y arrive pas...
lomdefer a écrit:f(x) = g(x) + h(x) ou f(x) = g(-x) -h(x).
Je ne comprends pas ce ou.
On a plutôt f(x)=g(x)+h(x) et f(-x)=g(x)-h(x).
Donc, d'après la première équation, g(x)=f(x)-h(x) et, d'après la deuxième, g(x)=f(-x)+h(x) donc f(x)-h(x)=f(-x)+h(x) donc 2h(x)=f(x)-f(-x) donc
Merci j'ai pu faire l'exo !!
Maitenant j'ai une autre question:
il faut montrer que toute fonction de R dans R se décompose toujours comme la différence de deux fonctions positives.
Je pense que c'est le même principe :
on pose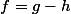 avec
avec 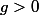 et
et 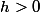
(1)=g(x)-h(x))
(2) j'arrive pas a trouver f(-x)
c'est g(x)+h(x) ou g(-x) + h(-x) ??
Maitenant j'ai une autre question:
il faut montrer que toute fonction de R dans R se décompose toujours comme la différence de deux fonctions positives.
Je pense que c'est le même principe :
on pose
(1)
(2) j'arrive pas a trouver f(-x)
c'est g(x)+h(x) ou g(-x) + h(-x) ??
Précisément, qu'est-ce que vous ne comprenez pas?
Prenons un exemple, peut-être que ce sera plus clair.
Soit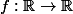 définie par :
définie par :
pour tout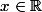 ,
, =e^x-1) .
.
Comment construire g et h deux fonctions réelles, positives, et telles que f=g-h (c'est-à-dire telles que pour tout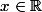 , f(x)=g(x)-h(x))?
, f(x)=g(x)-h(x))?
Pour construire ces deux fonctions, il suffit de dire quelle est l'image de x par g et h, pour tout x réel.
Soit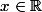 , alors trois cas peuvent se produire : soit f(x)>0, soit f(x)0, alors soit g(x)=f(x) et h(x)=0.
, alors trois cas peuvent se produire : soit f(x)>0, soit f(x)0, alors soit g(x)=f(x) et h(x)=0.
Si f(x)0 alors g(x)-h(x)=f(x)-0=f(x).
Si f(x)0, alors g(x)=f(x) 0.
0.
Si f(x) 0, alors g(x)=0
0, alors g(x)=0 0.
0.
(iii). h est-elle positive?
A vous de répondre...
Dans l'exemple, sauriez-vous me donner g et h? Et en général, quels sont leur graphe?
Prenons un exemple, peut-être que ce sera plus clair.
Soit
pour tout
Comment construire g et h deux fonctions réelles, positives, et telles que f=g-h (c'est-à-dire telles que pour tout
Pour construire ces deux fonctions, il suffit de dire quelle est l'image de x par g et h, pour tout x réel.
Soit
Si f(x)0 alors g(x)-h(x)=f(x)-0=f(x).
Si f(x)0, alors g(x)=f(x)
Si f(x)
(iii). h est-elle positive?
A vous de répondre...
Dans l'exemple, sauriez-vous me donner g et h? Et en général, quels sont leur graphe?
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

