Fonction lisses

[Sora03]

Bonjour , j'ai un exercice qui me pose un peu problème , est ce possible de m'aider s'il vous plait
Je dois sélectionner les réponses correctes

1)x3=o0(x)
2)x3=o0(x4)

3) 3x3=o0(x−x3)

4)x3=o0(x+x2)

Pour moi , la première est correcte car x^3 =o0(x²) donc o0(x) également

1)Si u(x)=o0(x5) et v(x)=o0(x5) alors u(x)−v(x)=o0(x5)
2)Si u(x)=o0(x5) et v(x)=o0(x4) alors u(x)−v(x)=o0(x5)

3)Si u(x)=o0(x4) et v(x)=o0(x5) alors 3u(x)−5v(x)=−5o0(x5)

4)Si u(x)=o0(x5) alors x^3u(x)=o0(x8)

5)Si u(x)=o0(x5) alors u(x)/x5=o0(x)

La quatrième est correcte selon moi car u(x)=x^4 donc x^3 * x^4 = x^7 o0(x^8)
après pour la cinquième u(x)=x^4 alors u(x)/x^5=x^4/x^5=1/x

Je ne sais pas si ce que j'ai fais est correcte , et pour les autres propositions je ne sais pas trop comment procéder .Merci d'avance pour votre aide

[anthony_unac]

Salut,
Peut être pourrais tu commencer par expliquer tes notations en rappelant la définition du petit o et du grand O.

[Sora03]

Les notations sont ceux de mon énoncé , je l'ai simplement recopier

[Sora03]

Mais on a vu qu'on pouvait aussi tout simplement l'écrire 0(x^5) par exemple

[Sora03]

C'est possible de m'aider du coup juste pour la deuxième partie des questions vu que je me suis finalement débrouiller pour la première

[GaBuZoMeu]

Je suis sûr que ton énoncé n'est pas écrit comme ça, avec des "o0".
Peut-être pour "petit o au voisinage de 0 ?

[Sora03]

Oui c'est exactement ça mais au moment de retranscrire j'ai un petit peu galérer

[Sora03]

1)Si u(x)= (x^5) et v(x)=petit o au voisinage de 0 (x^5) alors u(x)−v(x)=petit o au voisinage de 0(x^5)
2)Si u(x)=petit o au voisinage de 0 (x^5) et v(x)=petit o au voisinage de 0 (x^4) alors u(x)−v(x)=petit o au voisinage de 0 (x^5)

3)Si u(x)=petit o au voisinage de 0 (x^4) et v(x)=petit o au voisinage de 0 (x^5) alors 3u(x)−5v(x)=−5 petit o au voisinage de 0 (x^5)

4)Si u(x)=petit o au voisinage de 0 (x^5) alors x^3u(x)=petit o au voisinage de 0 (x^8)

5)Si u(x)=petit o au voisinage de 0 (x^5) alors u(x)/x^5=petit o au voisinage de 0 (x)


J'ai corrigé mon énoncé du coup

[GaBuZoMeu]

Tu as mangé un bout de l'énoncé pour 1)

D'accord, et qu'as-tu fait avec cet énoncé ? Un petit conseil : si tu n'est pas très à l'aise avec le maniement du "petit o", tu peux remplacer "petit o de x^n au voisinage de 0" par avec quand 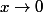(et éventuellement numéroter quand il y en a plusieurs.
Après, regrouper le tout en une puissance de x fois une fonction de x qui tend vers 0 quand x tend vers 0.

Exemple (tout est au voisinage de 0), plutôt que o(x²)+o(x³),

[Sora03]

Ah oui effectivement , d'accord , comme je l'ai dit plus haut

La quatrième me semble correcte car u(x)=x^4 donc x^3 * x^4 = x^7= petit o de (x^8) au voisinage de 0

après pour la cinquième u(x)=x^4 alors u(x)/x^5=x^4/x^5=1/x

mais je ne sais pas si c'est de cette manière là qu'il faut que je procède

[GaBuZoMeu]

x^7= petit o de (x^8) au voisinage de 0

Ah bon d'accord, selon toi on peut écrire x⁷ comme x⁸ fois une fonction de x qui tend vers 0 quand x tend vers 0 ????

[Sora03]

Je pensais que oui , vu que dans mon cours j'ai cet exemple x^4= petit o de (x^3) au voisinage de 0 lim x^4/x^3=0
quand x tend vers 0
mais en faite cette notation sert à calculer une limite c'est ça ?

[GaBuZoMeu]

M'enfin, fais attention !!!
Tu ne remarque pas que quand tu compares x⁴ et x³, 4 est plus grand que 3, tandis que quand tu compares x⁷ et x⁸, 7 est plus petit que 8 ?
avec 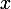qui tend vers 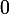quand 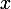tend vers (tautologique, n'est-ce pas ?), donc au voisinage de .

[Sora03]

Oui pardon c'est la fatigue , effectivement x^7=petit o de (x^6) au voisinage de 0

[Sora03]

Mais du coup pour les autres questions aussi je dois passer par les limites ?

[GaBuZoMeu]

Tu fais ce que tu veux, du moment que c'est correct.
Je t'ai indiqué un garde-fou, c'est tout.

[Sora03]

Mais je n'y arrive pas pour la 1,2,3

[Sora03]

Pour la 4ème voilà du coup : u(x)=x^6 alors x^3+x^6=x^9 soit petit o de (x^8) au voisinage de 0 donc la quatrième est vraie

et pour la cinquième u(x)=x^6 alors x^6/x^5=x donc la cinquième est fausse

[GaBuZoMeu]

Non. Si au voisinage de 0, ça ne veut pas dire que , voyons !
Je t'ai suggéré un moyen de ne pas te perdre. Je vois que tu n'en tiens aucun compte.

[Sora03]

Ah d'accord j'avais pas compris , du coup lim x^5-x^5 quand x tend vers 0 =0
et lim x^5 quand x tend vers 0 =0
donc la première proposition est vraie

lim x^5-x^4 quand x tend vers 0 = x^5(1-1/x)=+infini
et lim x^5 quand x tend vers 0=0
donc la proposition est fausse