Fonction de classe C infini

[jordvnsd]

Bonjour ,
Dans le cadre d'un devoir de niveau prepa mpsi je suis amené à montrer que: pour une certaine fonction f donnée ( de R dans R , dérivable) pour tout x dans R il existe b dans ]0;1[ tel que f(x)=f(0) +xf'(bx)

j'ai du mal à démarrer , pouvez vous me donner des indications svp
Merci d'avance

[mathelot]

Bonsoir,
ce résultat est le théorème des accroissements finis, qui se démontre grâce au théorème de Rolle.

Soit
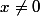
appliquer le théorème de Rolle , entre 0 et x, à la fonction de la variable t:



théorème de Rolle:
Soit f continue sur [a,b] , dérivable sur ]a,b[. On suppose f(a)=f(b)=0
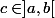
alors il existe tel que

[jordvnsd]

Merci beaucoup j'ai réussi à traiter cette question.
J'ai du mal a montrer que la fonction suivante : f(x)=1/(1+x^2) est 3*sqrt(3)/8 Lipschitzienne

[tournesol]

L'inégalité des accroissements finis permet de montrer que toute fontion à dérivée bornée sur un intervalle I
est ( sup sur I de |f'(x)| ) lipschitzienne . Ce sup est bien égal .

[jordvnsd]

Bonjour ,
Je suis confronté à la question suivante:
Montrer que le polynôme P=x^3 +x - 1 admet une unique racine réelle noté b , et que b appartient à l'intervalle [0;1] .
Je n'arrive pas à démarrer

[mathelot]

Bjr,
Montre que P est strictement croissant sur R.
Ce résultat est utile pour l'existence ou l'unicité d'une racine ?
Quel est le signe du produit P(0)P(1) ?
Ce résultat est utile pour l'existence ou l'unicité d'une racine ?

[jordvnsd]

Merci cela m'a été utile . Comment je pourrai me débrouiller pour montrer que b n'est pas un rationnel svp?

[jordvnsd]

Bonjour ,
J'ai montreé que: pour une certaine fonction f donnée ( de R dans R , dérivable) pour tout x dans R il existe b dans ]0;1[ tel que f(x)=f(0) +xf'(bx).
J'aimerai avoir des indications pour prouver que si x est non nul alors b est unique.
bonne soirée

[mathelot]

Merci cela m'a été utile . Comment je pourrai me débrouiller pour montrer que b n'est pas un rationnel svp?

Par l'absurde , supposons que la racine de P , notée b, est rationnelle.
alors avec a entier relatif et c entier naturel non nul avec
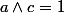
Montre alors que c|a (c divise a) (on remplace x par b dans le polynôme P)





attention : b signifie deux éléments distincts dans l'énoncé.

[mathelot]

Bonjour ,
J'ai montreé que: pour une certaine fonction f donnée ( de R dans R , dérivable) pour tout x dans R il existe b dans ]0;1[ tel que f(x)=f(0) +xf'(bx).
J'aimerai avoir des indications pour prouver que si x est non nul alors b est unique.
bonne soirée

on a: x non nul,



Peux tu donner l'expression de f ?

[jordvnsd]

Merci j'ai réussi grâce à vos indications .
Juste si je peux vous déranger pour une dernière question en lien avec ce qui précède.
Comment s'y prendre si on veut mq la suite Un définie par :U0=0 , Un+1=/(1+Un^2) converge vers b ?

[jordvnsd]

Merci cela m'a été utile . Comment je pourrai me débrouiller pour montrer que b n'est pas un rationnel svp?

Par l'absurde , supposons que la racine de P , notée b, est rationnelle.
alors avec a entier relatif et c entier naturel non nul avec
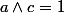
Montre alors que c|a (c divise a) (on remplace x par b dans le polynôme P)



Merci j'ai réussi grâce à vos indications .
Juste si je peux vous déranger pour une dernière question en lien avec ce qui précède.
Comment s'y prendre si on veut mq la suite Un définie par :U0=0 , Un+1=/(1+Un^2) converge vers b ?




attention : b signifie deux éléments distincts dans l'énoncé.

[jordvnsd]

merci

[jordvnsd]

Bonjour ,
J'ai montreé que: pour une certaine fonction f donnée ( de R dans R , dérivable) pour tout x dans R il existe b dans ]0;1[ tel que f(x)=f(0) +xf'(bx).
J'aimerai avoir des indications pour prouver que si x est non nul alors b est unique.
bonne soirée

on a: x non nul,



Peux tu donner l'expression de f ?

A droite on reconnais le taux d'accroissement au voisinage de 0.
Je ne suis pas sûr , f(x)=f(bx)?

[mathelot]

Merci beaucoup j'ai réussi à traiter cette question.
J'ai du mal a montrer que la fonction suivante : f(x)=1/(1+x^2) est 3*sqrt(3)/8 Lipschitzienne

donc f est contractante.
On a pour x,y positifs ou nuls

[mathelot]

Merci cela m'a été utile . Comment je pourrai me débrouiller pour montrer que b n'est pas un rationnel svp?

Par l'absurde , supposons que la racine de P , notée b, est rationnelle.
alors avec a entier relatif et c entier naturel non nul avec
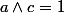
Montre alors que c|a (c divise a) (on remplace x par b dans le polynôme P)





attention : b signifie deux éléments distincts dans l'énoncé.

supposons tel que et


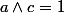
et
d'après un théorème de Gauss
a|c^2 puis a|c puis a|1 donc a=1
d'où


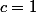
et
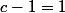
erreur. Donc la racine b du polynôme P n'est pas rationnelle.

[mathelot]

on veut mq la suite Un définie par :U0=0 , Un+1=/(1+Un^2) converge vers b ?

On a





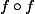
f est donc strictement décroissante et strictement croissante sur

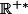
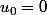
on étudie la suite définie par et



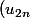croissante strictement



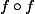
comme est strictement croissante sur:


...
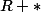
par récurrence.

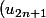décroissante strictement:
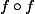
comme est strictement croissante sur :


..


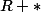
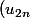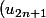donc strictement croissante et strictement décroissante.
Comme f est contractante
pour
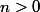
donc

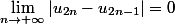
les deux sous suites sont adjacentes donc ont même limite
qui vérifie d'où

[jordvnsd]

Merci beaucoup j'ai réussi à traiter cette question.
J'ai du mal a montrer que la fonction suivante : f(x)=1/(1+x^2) est 3*sqrt(3)/8 Lipschitzienne

donc f est contractante.
On a pour x,y positifs ou nuls

[jordvnsd]

Merci beaucoup j'ai réussi à traiter cette question.
J'ai du mal a montrer que la fonction suivante : f(x)=1/(1+x^2) est 3*sqrt(3)/8 Lipschitzienne

donc f est contractante.
On a pour x,y positifs ou nuls

On m'avait suggéré l'inégalité des accroissement finis mais je n'arrive pas à montrer que
abs[-2x/(1+x^2)^2] < 3*sqrt(3)/8

[mathelot]

je n'arrive pas à montrer que
abs[-2x/(1+x^2)^2] < 3*sqrt(3)/8

re,
il suffit d'étudier le signe de f'' et le tableau des variations de f' sur