Bonjour,
Soit f de R+ dans R de classe C1 telle que f+f' est de carré intégrable.
Montrer que:
- f bornée
- f tend vers 0 en +infini
J'ai montré que f est bornée sans grandes difficultés mais je bloque sur la deuxième question. Il faudrait déjà montrer que f converge... Mais on ne sait même pas si f est de carré intégrable. Il doit me manquer un résultat intermédiaire que je ne vois pas. Qqn pourrait m'aider ? Merci
Fonction de carré intégrable
13 messages
- Page 1 sur 1
Salut,
Le seul truc qui me vient à l'esprit me semble bien compliqué...
On pose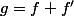 (continue) donc l'hypothèse devient
(continue) donc l'hypothèse devient 
Sauf que l'équa. diff.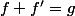 a pour solutions
a pour solutions =\Big(f(0)+\int_0^xg(t)e^t\,dt\Big)e^{-x}\) .
.
On a alors, par Cauchy-Schwarz,
|\leq |f(0)| e^{-x}+\int_0^x|g(t)|e^{t-x}\,dt\leq |f(0)| e^{-x}+\sqrt{\int_0^xg^2(t)\,dt}\sqrt{\int_0^xe^{2(t-x)}\,dt})
Et il suffit d'évaluer la deuxième intégrale pour conclure.
Edit : on conclue juste... que f est bornée.... mais pas plus.
Je pense qu'on peut conclure en écrivant|e^{t-x}\,dt=\int_0^A|g(t)|e^{t-x}\,dt+\int_A^x|g(t)|e^{t-x}\,dt) avec A bien choisi (puis 2 fois Cauchy-Schwarz) mais c'est surement pas la "bonne" méthode...
avec A bien choisi (puis 2 fois Cauchy-Schwarz) mais c'est surement pas la "bonne" méthode...
Le seul truc qui me vient à l'esprit me semble bien compliqué...
On pose
Sauf que l'équa. diff.
On a alors, par Cauchy-Schwarz,
Et il suffit d'évaluer la deuxième intégrale pour conclure.
Edit : on conclue juste... que f est bornée.... mais pas plus.
Je pense qu'on peut conclure en écrivant
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut,
Merci pour ton idée, mais comme on n'a pas encore fait les équations différentielles je ne pense effectivement pas que ce soit la bonne méthode.
Pour montrer que f bornée il y a beaucoup plus simple, il suffit d'intégrer^2=f^2+2ff'+f'^2) entre 0 et x
entre 0 et x
Je pense que le premier pas doit être de montrer que f converge, mais j'y bloque :/
Merci pour ton idée, mais comme on n'a pas encore fait les équations différentielles je ne pense effectivement pas que ce soit la bonne méthode.
Pour montrer que f bornée il y a beaucoup plus simple, il suffit d'intégrer
Je pense que le premier pas doit être de montrer que f converge, mais j'y bloque :/
Sauf erreur (en ce moment au niveau cervelle, ça va pas super fort...)
Si on pose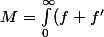^20) , on a
, on a
\geq\int_0^x(f+f')^2 +f^2(0)=\int_0^xf^2+\int_0^xf'^2+f^2(x))
Et comme les 3 termes de droite sont positifs, ça te vend que\leq M+f^2(0)) (donc
(donc  est bornée)
est bornée)
mézossi que) et comme
et comme  est une fonction croissante, cela prouve qu'elle a une limite en
est une fonction croissante, cela prouve qu'elle a une limite en  , c'est à dire que
, c'est à dire que 
Idem pour
Sinon, j'ai regardé, ça marche en utilisant l'indic. que j'ai donné plus haut, mais... il y a peut-être plus simple...
Si on pose
Et comme les 3 termes de droite sont positifs, ça te vend que
mézossi que
Idem pour
Sinon, j'ai regardé, ça marche en utilisant l'indic. que j'ai donné plus haut, mais... il y a peut-être plus simple...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Pas forcément : on ne peut pas dire que ce soit un résultat super utile (et le résultat est clairement faux dans le cas de f+g à la place de f+f')Charmander a écrit:Et puis je veux dire ça se saurait, siintégrable impliquait
intégrable
non, vu que le fait que f² soit intégrable sur [0,+oo] n'implique même pas qu'elle est bornée (même en la supposant C1, voire plus)Charmander a écrit:l'exercice perdrait son sens, on aurait pu utiliser ce résultat puis conclure en deux lignes
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ah oui, je vois... Je suis d'accord avec ta démonstration de l'intégrabilité de 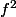 et
et  . Du coup
. Du coup 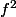 qui est une somme d'intégrales convergentes converge. Et une fois qu'on a ça on peut conclure puisque
qui est une somme d'intégrales convergentes converge. Et une fois qu'on a ça on peut conclure puisque 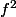 intégrable ET
intégrable ET 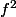 converge implique
converge implique 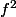 converge vers 0 (sinon, à partir d'un certain rang f est minorée par une constante qui n'est pas intégrable en +infini). Merci pour ton aide !
converge vers 0 (sinon, à partir d'un certain rang f est minorée par une constante qui n'est pas intégrable en +infini). Merci pour ton aide !
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
