Famille libre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ludo60
- Membre Relatif
- Messages: 114
- Enregistré le: 15 Nov 2015, 16:25
-
 par ludo60 » 12 Jan 2019, 15:31
par ludo60 » 12 Jan 2019, 15:31
Bonjour, on considère une famille

de vecteurs libres dans un e.v E.
On rajoute un vecteur à cette famille, noté
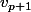
de sorte que la famille

soit liée.
Le but est alors de montrer que

.
J'ai réussi à montrer qu'au moins un des vecteurs s'exprime comme CL des autres mais ne comprends pas pourquoi ce vecteur est nécessairement
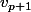
.
Merci pour votre aide.
-
Mimosa
- Membre Relatif
- Messages: 432
- Enregistré le: 19 Aoû 2016, 16:31
-
 par Mimosa » 12 Jan 2019, 15:54
par Mimosa » 12 Jan 2019, 15:54
Bonjour
Il existe des scalaires non tous nuls, tels que

.
Si

, la famille initiale étant libre, on a

, donc

et

, ce qui entraine

, donc

.
Si

, on multiplie par

et on a
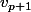
combinaison linéaire des autres.
-
ludo60
- Membre Relatif
- Messages: 114
- Enregistré le: 15 Nov 2015, 16:25
-
 par ludo60 » 12 Jan 2019, 16:33
par ludo60 » 12 Jan 2019, 16:33
Merci pour ta réponse. Je n'ai pas bien compris une partie:
Tu dis que si

, alors tous les

sont nuls. Ça, je vois bien.
Ne peut-on pas simplement dire alors que puisque les vecteurs sont liés, il existe nécessairement

puis conclure sur ta dernière phrase ?
-
Mimosa
- Membre Relatif
- Messages: 432
- Enregistré le: 19 Aoû 2016, 16:31
-
 par Mimosa » 14 Jan 2019, 15:05
par Mimosa » 14 Jan 2019, 15:05
C'est tout le problème que tu posais. Il y en a bien un non nul, mais pourquoi

?
-
ludo60
- Membre Relatif
- Messages: 114
- Enregistré le: 15 Nov 2015, 16:25
-
 par ludo60 » 15 Jan 2019, 15:18
par ludo60 » 15 Jan 2019, 15:18
Car s'il est nul, ils le sont tous ?
-
Mimosa
- Membre Relatif
- Messages: 432
- Enregistré le: 19 Aoû 2016, 16:31
-
 par Mimosa » 15 Jan 2019, 15:46
par Mimosa » 15 Jan 2019, 15:46
Oui, c'est ça.
-
ludo60
- Membre Relatif
- Messages: 114
- Enregistré le: 15 Nov 2015, 16:25
-
 par ludo60 » 15 Jan 2019, 15:49
par ludo60 » 15 Jan 2019, 15:49
ok, merci pour ton aide, j'y vois plus clair

-
Mimosa
- Membre Relatif
- Messages: 432
- Enregistré le: 19 Aoû 2016, 16:31
-
 par Mimosa » 15 Jan 2019, 16:14
par Mimosa » 15 Jan 2019, 16:14
-
mathelot
 par mathelot » 15 Jan 2019, 16:19
par mathelot » 15 Jan 2019, 16:19
pour résumer:
il existe une combinaison linéaire non triviale des
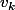
pour


ne peut pas être nul
donc
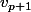
est combinaison linéaire des
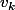
pour
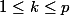
ainsi, on voit qu'une partie libre maximale (au sens de l'inclusion) est une famille génératrice.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités