Famille libre

par **med bah** » 23 Fév 2014, 14:57

bonjour tout le monde. .
j'ai vu dans un livre l'exo suivant:
fa:]0,1[ ====>R
x ==== > 1/(1-ax)
avec a appartenant à ]0,1[
ce qui est demandé est de montrer que cette famille de fonctions est libre .
je ne vois pas comment faire ,je n'arrive pas à prouver que les coefficients sont nuls
Merci pour votre aide .

par **adrien69** » 23 Fév 2014, 15:16

Salut,
Si tu prends une sous famille finie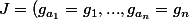

où les

sont pris par ordre croissant, et que tu poses

, comment se comporte f près de

pour chaque i pris l'un après l'autre ?
Qu'en déduis-tu si tu imposes que f doit être identiquement nulle ?

D'ailleurs ta fonction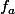

a un domaine de définition qui ne correspond pas.

par **adrien69** » 23 Fév 2014, 15:22

Autre méthode : on multiple par

On a alors k(x)*g(x) qui est un polynôme de degré n-1 exprimé dans la base de Lagrange associée au

avec pour coefficients

, il est censé être identiquement nul, les

ne l'étant pas, ça implique que les

sont tous nuls.

par **med bah** » 23 Fév 2014, 15:33

en ce qui concerne le domaine de définition de f ,c'est ça en fait qui me craie problème .
j'ai en fais passer un terme de l'autre côté et j'essaye de faire tendre x vers 1/a.
sauf que notre X ne peut pas tendre vers 1/a .
car x varie entre 0 et 1 or 1/a est dans ]1,+infini[

par **adrien69** » 23 Fév 2014, 15:36

Autre méthode,

On développe en série entière sur le domaine de plus petite convergence, i.e le plus petit des

sera notre borne.

, j'ai direcement inversé les sommes et mis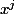

en facteur.

g doit valoir 0 identiquement, donc toutes ses dérivées en 0 doivent valoir 0, or elles sont données par

Si on suppose les

non tous nuls, cela équivaut à dire que les lignes

sont liées. Et donc que le déterminant de Vandermonde de

est nul. Sauf que les

sont distincts, et que donc c'est faux. Donc les

sont tous nuls.

par **med bah** » 23 Fév 2014, 15:41

Merci beaucoup pour votre aide :) .

par **adrien69** » 23 Fév 2014, 15:41

med bah a écrit:en ce qui concerne le domaine de définition de f ,c'est ça en fait qui me craie problème .
j'ai en fais passer un terme de l'autre côté et j'essaye de faire tendre x vers 1/a.
sauf que notre X ne peut pas tendre vers 1/a .
car x varie entre 0 et 1 or 1/a est dans ]1,+infini[

Y a peut-être simplement une erreur d'énoncé.

par **adrien69** » 23 Fév 2014, 15:55

Une autre méthode, si

, c'est vrai pour l'intégrale de 0 à x (tant qu'on reste dans le bon domaine).

, ici on utilise

positif pour tout i donc on restraint x

Ici il faut traiter le cas : et si tous les

sont des entiers (polynôme constant implique)?
On en déduit quoi pour les rationnels (multiplier par le PPCM des dénominateurs)?
Puis pour les réels (par densité, mais c'est difficile).
Et on a fini.

par **adrien69** » 23 Fév 2014, 15:57

J'ai essayé de trouver une équation différentielle linéaire que vérifiait tout le monde, histoire d'utiliser le Wronskien et l'indépendance en un point pour montrer l'indépendance partout, mais je n'y arrive pas encore :/

par **Ben314** » 23 Fév 2014, 16:19

med bah a écrit:sauf que notre X ne peut pas tendre vers 1/a .
car x varie entre 0 et 1 or 1/a est dans ]1,+infini[

Ca ne pose pas de problème : si une fraction rationelle est nulle sur un ensemble infini, alors elle est nulle sur tout son ensemble de définition (car c'est vrai pour les polynômes et qu'une fraction rationelle est nulle ssi son numérateur est nul)

Donc la solution de loin la plus simple est bien de faire tendre x vers chacun des 1/a_i

par **med bah** » 23 Fév 2014, 17:50

oui j'ai saisie ton idée Ben314 . c'est bien dit . tout a fait d'accord avec toi la fraction sera donc défini sur R\{1/a1;1/a2...;1/an} . tendre x vers 1/ai devient possible . Merci :++:

Famille libre

famille libre

Qui est en ligne