Famille libre polynôme de degrés 2 à 2 distinct
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
JSDOS
- Messages: 1
- Enregistré le: 25 Juil 2022, 11:05
-
 par JSDOS » 25 Juil 2022, 11:25
par JSDOS » 25 Juil 2022, 11:25
Bonjour,
Je dois démonter que toute famille de polynôme de degrés 2 à 2 distinct est libre.
Est-ce que ça marche en montrant qu’une famille composée d’un polynôme de degrés 1 (constante) est libre et que pour toute famille de polynôme de degrés 2 à 2 distinct libre auquel on ajoute un polynôme de degrés supérieur alors la combinaison linaire nul demande que le dernier terme sois nul or le polynôme du degré le plus élevé est non nul donc son coefficient est nul, la famille est libre.
Merci beaucoup d’avance

-
Ayzee
- Membre Naturel
- Messages: 12
- Enregistré le: 18 Aoû 2022, 09:26
-
 par Ayzee » 21 Aoû 2022, 11:11
par Ayzee » 21 Aoû 2022, 11:11
Tu reviens simplement à la définition d'une famille libre en supposant qu'il existe une combinaison linéaire de polynômes de degré deux à deux distincts nulle. En identifiant les coefficients avec le polynôme constant nul, tu peux conclure très facilement! Et si tu bloques encore cette question a déjà été posée il me semble sur le forum.
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 21 Aoû 2022, 12:44
par lyceen95 » 21 Aoû 2022, 12:44
toute famille de polynôme de degrés 2 à 2 distinctComment on lit cette phrase, il manque un 2 ? toute famille de polynôme de degré 2 2 à 2 distinct
Et les polynômes
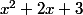
et
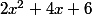
sont distincts, mais pour autant, ils ne forment pas une famille libre.
-
Ayzee
- Membre Naturel
- Messages: 12
- Enregistré le: 18 Aoû 2022, 09:26
-
 par Ayzee » 21 Aoû 2022, 14:26
par Ayzee » 21 Aoû 2022, 14:26
Il doit sûrement parler d'une famille de polynômes à degré échelonné!
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 22 Aoû 2022, 08:13
par lyceen95 » 22 Aoû 2022, 08:13
Oui, tu as raison.
Ce ne sont pas les polynômes qui sont distincts, ce sont les degrés des polynômes.
Mon erreur m'a sauté aux yeux en revoyant le titre de la discussion.
Donc, le matin, je suis plus 'réveillé' que l'après midi, à l'heure de la sieste !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
