Extrema fonction
20 messages
- Page 1 sur 1
Extrema fonction
Bonjour,
J'aimerais vos avis sur un exo en rapport aux dérivées partielles.
Soit une fonction de E, sous-ensemble de Rn, dans R, je cherche ses extremums.
L'ensemble est compact et la fonction continue, donc ils existent.
Cependant, le sous-ensemble E ne se caractérise pas par une equation, mais pas une inéquation.
Donc impossible d'utiliser le théorème des fonctions implicite ou la méthode des multiplicateurs de Lagrange.
Comment procédé ?
Exemple : n=2, E=disque fermé de rayon 1 (donc inéquation : X^2+Y^2<=1)
et f(x,y)=(x+y)/(1+x^2+y^2)
Merci
J'aimerais vos avis sur un exo en rapport aux dérivées partielles.
Soit une fonction de E, sous-ensemble de Rn, dans R, je cherche ses extremums.
L'ensemble est compact et la fonction continue, donc ils existent.
Cependant, le sous-ensemble E ne se caractérise pas par une equation, mais pas une inéquation.
Donc impossible d'utiliser le théorème des fonctions implicite ou la méthode des multiplicateurs de Lagrange.
Comment procédé ?
Exemple : n=2, E=disque fermé de rayon 1 (donc inéquation : X^2+Y^2<=1)
et f(x,y)=(x+y)/(1+x^2+y^2)
Merci
adrien69 a écrit:Salut,
Ton extrema existe, mais peut-il être atteint à l'intérieur du disque ?
Je cherche les extremums de la fonction, à l'intèrieur du disque. Ces extremums existe car le disque est un ensemble compacte et la fonction est continue.
(Je ne cherche pas les extremums globaux de la fonction, qui ne sont évidemment pas dans le disque)
Il faut voir le disque comme une contrainte sur la fonction.
salut
cherche les points critiques de f ... y en a-t-il dans le disque unité ?
ou
passe en polaire
d'autre part en remarquant que f(x, y) = f(y, x) si extremum alors il se trouve sur la droite d'équation y = x
de même on voit que f(-x, -y) = -f(x, y) donc si max alors min ....
....
cherche les points critiques de f ... y en a-t-il dans le disque unité ?
ou
passe en polaire
d'autre part en remarquant que f(x, y) = f(y, x) si extremum alors il se trouve sur la droite d'équation y = x
de même on voit que f(-x, -y) = -f(x, y) donc si max alors min ....
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
@Adrien : Au temps pour moi, l'extrema est sur la frontière et pas à l'intèrieur, d'où ta question. Mais comme je l'ai dit mon ensemble est constitué des 2 donc peut importe .. C'est mon exemple qui est nul (trop particulier). Enfaite je cherche un méthode générale pour pouvoir gérer les inéquations comme contraintes..
@Zigomatique : Les deux règles que tu me donnes me paraissent étranges ... Peut tu développer please ? (surtout la deuxième, qui me parait fausse même dans l'exemple)
@Zigomatique : Les deux règles que tu me donnes me paraissent étranges ... Peut tu développer please ? (surtout la deuxième, qui me parait fausse même dans l'exemple)
Dans tous les cas tu devras étudier le problème sur l'intérieur dans ce genre de cas. Et ensuite travailler sur la frontière, qui localement s'exprime comme h(x)=0, via les fonctions implicites. Et dès lors tu peux utiliser les extremas liés (et les multiplicateurs de Lagrange). Du moins si j'ai bien compris ta question.
oui je suis d'accord pour ton exemple .... mais ta solution vaut tout autant que de prendre x = y = -pi/4 .... et je ne dis pas qu'il n'y en a pas ailleurs .... du fait des propriétés de la fonctions sinus .... en particulier sa périodicité ....
en particulier une fois vu que f(x, y) est maximal en (-pi/4,-pi/4) alors pour tout t = -pi/4 + mpi/3 et u = -pi/4 +npi/3 avec (m, n) parcourant ZxZ f(t, u) est maximal ....
ma démo concernait l'énoncé initial ...
en particulier une fois vu que f(x, y) est maximal en (-pi/4,-pi/4) alors pour tout t = -pi/4 + mpi/3 et u = -pi/4 +npi/3 avec (m, n) parcourant ZxZ f(t, u) est maximal ....
ma démo concernait l'énoncé initial ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Salut,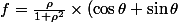\) et ton domaine aussi :
et ton domaine aussi :  ,
,  quelconque.
quelconque.
Conclusion : ce n'est pas vraiment un problème "en dimension 2" vu qu'il suffit de chercher le max de deux fonctions de R dans R.
Vu la tête de ton domaine et de ta fonction, je m'embêterais pas avec avec des truc théoriques : en polaire, ta fonction est "à variables séparées" :solr a écrit:Exemple : n=2, E=disque fermé de rayon 1 (donc inéquation : X^2+Y^2<=1)
et f(x,y)=(x+y)/(1+x^2+y^2)
Conclusion : ce n'est pas vraiment un problème "en dimension 2" vu qu'il suffit de chercher le max de deux fonctions de R dans R.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
